Q-Learning

Q-learning [Watkins,1989] is a recent form of Reinforcement Learning algorithm that does not need a model of its environment and can be used on-line.

The algorithm

Let the world state at time

be

, and assume that the learning system then chooses action

. The immediate result is that a reward

is received by the learner and the world undergoes a transition to the next state $x_{t+1}$ . The objective of the learner is to choose actions maximizing discounted cumulative rewards over time. More precisely, let $\gamma$ be a specified discount factor in $[0 \; 1)$ . The total discounted return (or simply return) received by the learner starting at time

is given by:

$\displaystyle r_{(t)}= r_t+ \gamma r_{t+1}+ \gamma^2 r_{t+2}+\cdots+\gamma^n r_{t+n}+ \cdots$

(1)

The discount factor $\gamma$ is a number in the range of

and is used to weight near term reinforcement more heavily than distant future reinforcement. The closer $\gamma$ is to

the greater the weight of future reinforcements.

The objective is to find a policy $\pi$ , or rule for selecting actions, so that the expected value of the return is maximized. It is sufficient to restrict attention to policies that select actions based only on the current state (called stationary policies) : $\pi(x_t)=a_t$ . For any such policy $\pi$ and for any state we define:

$\displaystyle V^\pi (x) = E\{ r_{(0)} \vert x_0 = x; a_i = \pi(x_i)$ for all $\displaystyle i \geq 0 \}$

(2)

The expected total discounted return received when starting in state x and following policy $\pi$ thereafter. If $\pi$ is an optimal policy we also use the notation for $V^\pi$ . Many dynamic programming-based reinforcement learning methods involve trying to estimate the state values or $V^\pi (x)$ for a fixed policy $\pi$ .

Q-learning, is a simple incremental algorithm developed from the theory of dynamic programming [Ross,1983] for delayed reinforcement learning. In Q-learning, policies and the value function are represented by a two-dimensional lookup table indexed by state-action pairs. Formally, for each state and action let:

$\displaystyle Q^*(x, a)$	$\displaystyle =$	$\displaystyle E\{r_0 + \gamma V^*(x_1) \vert x_0 =x; a_0 = a \}$	(3)
	$\displaystyle =$	$\displaystyle R(x,a) + \gamma \sum_y P_{xy}(a) V^* (y)$	(4)

where $R(x, a) = E\{r_0 \vert x_0 =x; a_0 = a \}$ and $P_{xy}(a)$ is the probability of reaching state as a result of taking action in state . It follows that

$\displaystyle \displaystyle V^*(x) = \max_a Q^*(x,a)$

(5)

Intuitively, Equation 4 says that the state-action value,

, is the expected total discounted return resulting from taking action

in state

and continuing with the optimal policy thereafter. More generally, the

function can be defined with respect to an arbitrary policy $\pi$ as

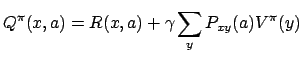$\displaystyle Q^\pi (x, a) = R(x,a) + \gamma \sum_y P_{xy}(a) V^\pi (y)$

(6)

and

is just $Q^\pi$ for an optimal policy $\pi$ .

The Q-learning algorithm works by maintaining an estimate of the function, which we denote by $\hat{Q}^*$ , and adjusting $\hat{Q}^*$ values (often just called Q-values) based on actions taken and reward received. This is done using Sutton's prediction difference, or TD error [Sutton,1988] - the difference between (the immediate reward received plus the discounted value of the next state) and (the Q-value of the current state-action pair):

$\displaystyle r + \gamma \hat{V}^*(y) - \hat{Q}^*(x,a)$

(7)

where

is the immediate reward,

is the next state resulting from taking action

in state

, and $\hat{V}^*(x) = \max_a \hat{Q}^*(x,a)$ . Then the values of $\hat{Q}^*$ are adjusted according to

$\displaystyle \hat{Q}^*(x,a) = (1-\alpha) \hat{Q}^*(x,a) + \alpha (r + \gamma \hat{V}^*(y))$

(8)

where $\alpha \in (0 \; 1]$ is a learning rate parameter. Note that the current estimate of the function implicitly defines a greedy policy by $\displaystyle \pi(x) = arg \max_a \hat{Q}^*(x,a)$ . That is, the greedy policy is to select actions with the largest estimated Q-value.

It is important to note that the Q-learning method does not specify what actions the agent should take at each state as it updates its estimates. In fact, the agent may take whatever actions it pleases. This means that Q-learning allows arbitrary experimentation while at the same time preserving the current best estimate of states' values. This is possible because Q-learning constructs a value function on the state-action space, instead of the state space. It constructs a value function on the state space only indirectly. Furthermore, since this function is updated according to the ostensibly optimal choice of action at the following state, it does not matter what action is actually followed at that state. For this reason, the estimated returns in Q-learning are not contaminated by "experimental" actions [Watkins,1989], so Q-learning is not experimentation-sensitive.

To find the optimal Q function eventually, however, the agent must try out each action in every state many times. It has been shown [Watkins,1989 ; Dayan,1992] that if equation 8 is repeatedly applied to all state-action pairs in any order in which each state-action pair's Q-value is updated infinitely often, then $\hat{Q}^*$ will converge to and $\hat{V}^*$ will converge to with probability 1 as long as $\alpha$ is reduced to 0 at a suitable rate. This is why the policy $\pi(x) = arg \max_a \hat{Q}^*(x,a)$ is only used a part of the time in order to be able to explore the state-action space completely. At each iteration , we will choose to make either a random action random or the optimal action $a_i=\pi(x_i)$ . We will take the first possibility (the random action) with a probability of $\epsilon$ . At the beginning of the learning $\epsilon$ must be huge (near 1). At the end of the learning, when $\hat{Q}^* \approx Q^*$ , we will set $\epsilon=0$ to always use the optimal policy. It is, as always, the compromise between exploitation-exploration.

Shortly, we have:

$\alpha$ : learning rate
$\gamma$ : discount factor The closer $\gamma$ is to the greater the weight is given to future reinforcements.
$\epsilon$ : probability to use a random action instead of the optimal policy.

The robot Applet.

An illustration of these concepts is the robot example. At each time step, the robot can choose one of the following action:

move its arm (yellow line) up.
move its arm (yellow line) down.
move its hand (red line) right.
move its hand (red line) left.

The reward the robot gets is simply the number of pixel on the screen it has moved (positive values for movement to the right and negative values for movement to the left). The goal is that the robot move to the right the faster possible

.

Some remarks:

You can see on the upper-left part of the screen the average speed of the robot. That is:

average speed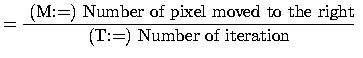 $\displaystyle = \frac{\text{ (M:=) Number of pixel moved to the right}}{\text{(T:=) Number of iteration}}.$ (9)

When you press the [reset speed counter] button, the program set and .
Small value of $\gamma$ will not allow the robot to extend its arm forward to the right because during all this time the robot gets no reward. You must set a high value for $\gamma$ otherwise the robot doesn't see that, far in the future, it is useful to have its arm extended.
$\epsilon$ should be set a high value (.8) at the beginning of the learning process. $\epsilon$ should be set to zero when the optimal control policy has been found. To see if an optimal policy has been found, press the [reset speed counter] button and wait a little until the [speed counter] stabilizes. You have now a correct evaluation of the speed of the robot. Continue the learning process until you can't increase this value anymore.
You can compete with the algorithm! See by yourself that the Q-learning is the best! Try to beat it! How to play? Press the [stop] button. Press the [reset speed counter] button. Move the arm and the hand of the robot using the 4 arrow keys: [UP/DOWN] moves the arm (yellow line) and [LEFT/RIGHT] move the hand (red line). Move the robot until the [speed counter] stabilizes. Now the result: Do you really go faster than Q-learning?

Bibliography

[Ross,1983] Ross, S. (1983). Introduction to Stochastic Dynamic

[Sutton,1988] Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Machine Learning 3:9-44.
[Watkins,1989] Watkins,C. (1989). Learning from Delayed Rewards,Thesis,University of Cambridge,England.
[Dayan,1992] Dayan, P. (1992). The convergence of TD( $\lambda$ ) for general $\lambda$ . Machine Learning 8:117-138.

Download&links

The JAR-file of the applet (which can also be run as a stand-alone program) is here.
The source code of the applet is here (1 file).
The mathematical parts of this page are downloadable in PDF.

Reinforcement Learning Repository : you will find there an excellent illustrated tutorial which is mirrored here.
You can download A short Introdution to Reinforcement Learining by Stephan ten Hagen and Ben Kröse.
The on-line book by Sutton & Barto Book,"Reinforcement Learning: an introduction" is mirrored here.
A link to a Reinforcement Learning site