Classification Trees: C4.5

Tree Generation: Gain criteria.

business-insight
Imagine selecting one example at random from a set $ T$ of training examples and announcing it belongs to the class $ C_i, \; i=1,\ldots,k$. This message has the probability:

$\displaystyle \frac{\vert C_i\vert}{\vert T\vert}$ (1)

business-insight
Where $ \vert C_i\vert$ is the number of examples which belongs to the class $ C_i$. The information contained in this announce is:

$\displaystyle - \log_2 \frac{\vert C_i\vert}{\vert T\vert}$   bits. (2)

In general, if we are given a probability distribution $ P = (p_1=\frac{\vert C_1\vert}{\vert T\vert} , p_2=\frac{\vert C_2\vert}{\vert T\vert} , .., p_k=\frac{\vert C_k\vert}{\vert T\vert} )$ then the Information conveyed by this distribution (also called the Entropy of P), is:

$\displaystyle I(P) = - \sum_{i=1}^k p_i*\log(p_i)$ (3)

When applied to the set $ T$ of training example, $ I(P)$ measures the average amount of information (bits) needed to identify the class of an example of $ T$ (it's a weighted sum of the $ k$ different equations 2).

For example, if $ P$ is $ (0.5, 0.5)$ then $ I(P)$ is 1, if P is $ (0.67, 0.33)$ then $ I(P)$ is 0.92, if P is $ (1, 0)$ then $ I(P)$ is 0. [Note that the more uniform is the probability distribution, the greater is its information.]

An other example: We want to known if a golfer will play or not based on the following data: 

    OUTLOOK | TEMPERATURE | HUMIDITY | WINDY | PLAY
    =====================================================
    sunny   |      85     |    85    | false | Don't Play
    sunny   |      80     |    90    | true  | Don't Play
    overcast|      83     |    78    | false | Play
    rain    |      70     |    96    | false | Play
    rain    |      68     |    80    | false | Play
    rain    |      65     |    70    | true  | Don't Play
    overcast|      64     |    65    | true  | Play
    sunny   |      72     |    95    | false | Don't Play
    sunny   |      69     |    70    | false | Play
    rain    |      75     |    80    | false | Play
    sunny   |      75     |    70    | true  | Play
    overcast|      72     |    90    | true  | Play
    overcast|      81     |    75    | false | Play
    rain    |      71     |    80    | true  | Don't Play

We will build a classifier which, based on the features OUTLOOK, TEMPERATURE, HUMIDITY and WINDY will predict wether or not the golfer will play. There are 2 classes: (play) and (don't play). There are 14 examples. There are 5 examples which gives as result "don't play" and 9 examples which gives as result "will play."

We will thus have $ Info(T) = I(9/14, 5/14) = 0.94$

Consider a similar measurement after $ T$ has been partitioned in accordance with the $ n$ outcomes of a test on the feature X. (in the golfer example, X can be a test on OUTLOOK, TEMPERATURE, ...). The expected information requirement can be found as a weighted sum over the subsets:

$\displaystyle Info(X,T) = \sum_i^n \frac{\vert T_i\vert}{\vert T\vert} Info(T_i)$ (4)

where $ {T_1, T_2, \ldots ,T_m}$ is the partition of T induced by the value of $ X$.

In the case of our golfing example, for the attribute Outlook we have:

$\displaystyle Info(Outlook,T) = 5/14*I(2/5,3/5) + 4/14*I(4/4,0) + 5/14*I(3/5,2/5) = 0.694$ (5)

Consider the quantity $ Gain(X,T)$ defined as:

$\displaystyle Gain(X,T) = Info(T) - Info(X,T)$ (6)

This represents the difference between the information needed to identify an element of T and the information needed to identify an element of T after the value of attribute X has been obtained, that is, this is the gain in information due to attribute X.

In our golfing example, for the Outlook attribute the gain is:

$\displaystyle Gain(Outlook,T) = Info(T) - Info(Outlook,T) = 0.94 - 0.694 = 0.246.$ (7)

If we instead consider the attribute Windy, we find that $ Gain(Windy,T)=0.048$. Thus OUTLOOK offers a greater informational gain than WINDY.

We can use this notion of gain to rank attributes and to build decision trees where at each node is located the attribute with greatest gain among the attributes not yet considered in the path from the root.

In the Golfing example we will obtain the following decision tree: 


                        Outlook
                       / |     \
                      /  |      \
            overcast /   |sunny  \rain
                    /    |        \
               Play    Humidity   Windy
                     /   |         |  \
                    /    |         |   \
              <=75 /  >75|     true|    \false
                  /      |         |     \
                 Play   Don'tPlay Don'tPlay Play

Tree Generation: Gain_Ratio criteria.

The notion of Gain introduced earlier tends to favor test on features that have a large number of outcomes (when $ n$ is big in equation 4). For example, if we have a feature $ X$ that has a distinct value for each record, then $ Info(X,T)$ is 0, thus $ Gain(X,T)$ is maximal. To compensate for this Quinlan suggests using the following ratio instead of Gain:

GainRatio(X,T)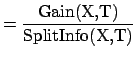$\displaystyle =\frac{\text{Gain(X,T)}}{\text{SplitInfo(X,T)}}$ (8)

Consider the information content of a message that indicate not the class to which the case belongs, but the outcome of the test on feature $ X$. By analogy with equation 3, we have

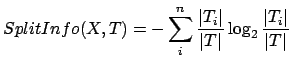$\displaystyle SplitInfo(X,T)= - \sum_i^n \frac{\vert T_i\vert}{\vert T\vert} \log_2 \frac{\vert T_i\vert}{\vert T\vert}$ (9)

The $ GainRatio(X,T)$ is thus the proportion of information generated by the split that is useful for the classification.

In the case of our golfing example $ GainRatio(OUTLOOK,T)=0.246/1.577 = 0.156$ and $ GainRatio(WINDY,T)=0.048/0.985 = 0.049$.

We can use this notion of $ GainRatio$ to rank attributes and to build decision trees where at each node is located the attribute with greatest $ GainRatio$ among the attributes not yet considered in the path from the root.

We can also deal with the case of features with continuous ranges. Say that feature $ X$ has a continuous range. We examine the values for this features in the training set. Say they are, in increasing order, $ A_1, A_2, \ldots, A_m$. Then for each value $ A_j, \; j=1,2,..m$ we partition the records into 2 sets : the first set have the $ X$ values up to and including $ A_j$ and the second set have the $ X$ values greater than $ A_j$. For each of these $ m$ partitions we compute the $ GainRatio(X(j),T) \; j=1,2,..m$, and choose the partition that maximizes the gain. If all features are continuous, we will obtain a binary tree.

Pruning Trees.

Pruning a tree is the action to replace a whole subtree by a leaf. The replacement takes place if the expected error rate in the subtree is greater than in the single leaf. We will start by generating the whole (generally overfitted) classification tree and simplify it using pruning just after.

The error estimates for leaves and subtrees are computed assuming that they were used to classify a set of unseen cases of the same size as the training set. So a leaf covering $ N$ training cases ($ E$ of them incorrectly) with a predicted error rate of $ U_{CF}(E,N)$ (with $ U_{CF}$: the binomial distribution, $ CF$: the Confidence Level) would give rise to a predicted $ N \times U_{CF}(E,N)$ errors. Similarly, the number of predicted errors associated with a (sub)tree is just the sum the the predicted errors of its branches.

An example: Let's consider a dataset of 16 examples describing toys. We want to know if the toy is fun or not. 

    COLOR   | MAX NUMBER OF PLAYERS | FUN
    =====================================================
    red     |  2                    | yes
    red     |  3                    | yes
    green   |  2                    | yes
    red     |  2                    | yes
    green   |  2                    | yes
    green   |  4                    | yes
    green   |  2                    | yes
    green   |  1                    | yes
    red     |  2                    | yes
    green   |  2                    | yes
    red     |  1                    | yes
    blue    |  2                    | no
    green   |  2                    | yes
    green   |  1                    | yes
    red     |  3                    | yes
    green   |  1                    | yes
We obtain the following classification tree: 
                   Color
                /    |     \
               /     |      \             pruning
          red /      |green  \blue   =================>    yes
             /       |        \
            yes     yes       no
          (leaf1)  (leaf2)   (leaf3)

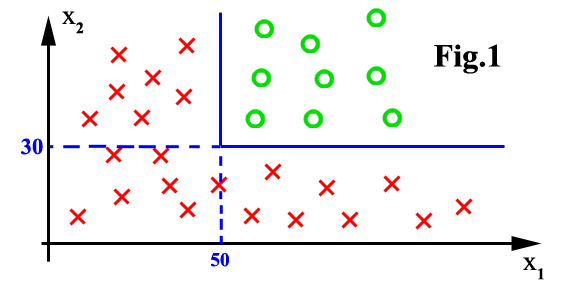
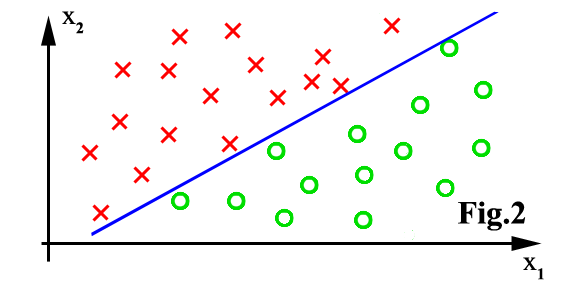
The predicted error rate for leaf 1 is $ 6 \times U_{25\%}(0,6)=6 \times 0.206$. The predicted error rate for leaf 2 is $ 9 \times U_{25\%}(0,9)=9 \times 0.143$. The predicted error rate for leaf 3 is $ 1 \times U_{25\%}(0,1)=1 \times 0.75$. The total number of predicted error for this subtree is $ 6 \times 0.206+9 \times 0.143+1 \times 0.75=3.273$. If the tree were replaced by the simple leaf "Yes", the predicted error rate would have been: $ 16 \times U_{25\%}(1,16)= 16 \times 0.157=2.512$. Since the simple leaf has a lower predicted error ( $ 2.512<3.273$), the tree is pruned to a leaf.

Limitations

The major limitation is that the feature space can only be partitioned in boxes parallel to axes of the space. There is no problem in figure 1, above. There will be bad classification accuracy in figure 2.

The implementation of the classification-tree algorithm I realized is only able to classify continuous features. This means, that it can only generate binary trees. We can still use the program with special discrete features like MAX NUMBER OF PLAYERS=(1,2,3,4) in the toy example above. We can use discrete features if they exhibit some ordering property. This means that discrete features like COLOR=(red,green,blue) are not allowed.

Bagging and Feature selection

We can use many classifiers and make a vote to obtain the final class of the examples we want to classify. How does it help? Let's assume you have 10 decision trees $ T_1, T_2, \ldots, T_{10}$. You want to make classification in 3 classes $ C_1, C_2, C_3$. Let's now assume that the first 4 trees $ T_1, \ldots, T_4$ always recognize and classify correctly class $ C_1$ (they are specialized for $ C_1$). The other trees are specialized in other classes. Let's now assume you want to classify a new example. This example belongs to $ C_1$. The trees $ T_1, \ldots, T_4$ will answer $ C_1$. The other trees will gives random answer which will form some "uniformly distributed noise" during the vote. The result of the vote will thus be $ C_1$. We just realized an error de-correlation.

How to generate the 10 trees? We don't have to know what are the specialty of each tree. We only have to build trees that have various behavior. We will build the 10 different trees using the algorithm previously described on 10 different sets of examples. How do we generate these 10 sets of example? We will use only a small part (called a bootstrap) of the full set of example (this technique is called BAGGING). Each bootstrap (there are here 10) will be build using random example taken from the full set of example (random selection with duplication allowed). We will also use a small subset of all the features available (this technique is called FEATURE SELECTION). For each bootstrap, we will use different randomly chosen features (random selection with duplication forbidden). The combination of BAGGING and FEATURE SELECTION is called BAGFS.

What's the optimal number of trees? Can we take the highest number possible? no, because another phenomena will appear: the OVERFITING. The classifier lose its generalization ability. It can only classify the examples which were used to build it. It cannot classify correctly unseen examples.

Bibliography

The excellent book of Quinlan.

Download

The mathematical parts of this page are downloadable in PDF.

business-insight
You can download here the source code of the latest version of the BAGFS_C4.5 toolbox. The code is relatively simple and has some limitations. There is a makefile for unix users, but the compilation under windows is also no problem: it's just standard C/C++ code without any special libaries. The toolbox includes utilities to build classifier (the number of bootstrap and the number of feature to use in BAGFS is found automatically using cross-validation techniques), to evaluate the performances (calculation of confusion matrix and kappa index), to compare different classifiers (using non-parametric test). You can also calculate a-priory distribution using a-posteriory distribution and a confusion matrix. There is a small test-file (data_gen) which will generate a dataset similar to the dataset seen in figure 1, so that you can easily test the code (There is noise inside this dataset: it will be removed using pruning techniques). The trees generated are saved in an ascii-form easily understandable by a human.