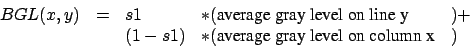Image Feature extraction for Classification purposes

Introduction

To classify an object in a image, we must first extract some features out of the image. We will use these features inside a classification tool like C4.5 (decision tree) to obtain the final class. I have made a small package to work with gray-level images (gray color coded on 8 bits). This package has been highly speed-optimized. For example, it uses some "tricks" of demo-coders to allow fast resize of images without any floating point operations nor multiplications (most of the time, one C intruction corresponds to one machine language instruction). All the scalings are done using a "resampling" algorithm (new pixels are the average of old pixels). Here is a small description of the capabilities of the package. It's currently used on-line in a real-time application to classify glass defects. If you are not interrested in the math, you can go directly to the end of the page to see fun examples.

Noise removal : ceiling

two parameters used: s1,s2.

To be able to filter correctly the image, we must know the value of the background gray level= BGL. This is an iterative algorithm. At each pass, the value of the BGL is refined. The BGL is calculated using the following algorithm (s1 is a parameter to give):

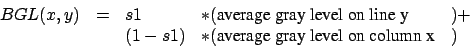$\begin{displaymath}\begin{array}{lllll} BGL(x,y) &=& s1 & * (\text{average gray... ... & * (\text{average gray level on column x} &) \\ \end{array}\end{displaymath}$

(1)

When we calculate the two above average we only use the points that belongs to the object we want to isolate. A point $C$ does NOT belong to the object if $(BGL-s2)<C<(BGL+s2)$ . The parameter s2 must be given. The average are thus calculated on set of points changing at each pass.

One last pass is done to re-center all the gray level to 128. For each point of the image, we execute:

(new gray level) $\displaystyle =$ (old gray level) $\displaystyle - BGL + 128$

(2)

Cropping

three parameters used: s3,s4,s5.

Let's consider an image with 3 white peaks. Two of these peaks belongs to the object to classify, the last one (far away from the 2 others) is noise. We want to crop the image so that only the object to classify remains.

The algorithms begins by searching the point $P_1$ which has the Gray Level the further away from 128 (128 is now the color of the background: see previous step: noise cancellation). This point $P_1$ will usually belong to one of the two peaks evoked before. From this point we will make a "special flood fill" (see end of the section to have a more precise description of the flood fill). The program draws a rectangular box around the zone which has been colored by the "flood fill". Everything outside this box is cropped.

Ideally, the "flood fill" should color the two right peaks. Unfortunately, there is very often, between these 2 peaks, a zone of the image at 128. This zone prevents the "flood fill" to expand up to the second peaks. To overcome this difficulty, the "flood fill" is executed on a reduced copy of the original image (horizontal scaling:s4, vertical scaling: s5). Based on this colored copy, we crop the original image.

FLOOD FILL: coloring algorithm.

The algorithm start from a given pixel. Then, It colors all the adjacent pixel. The coloring stops when we find a gray level $C$ such that $128-a < C <= 128+a$ with $a=abs(b-128)*s3$ and $b$ =gray level of point $P_1$ .

NOTE: This algorithms works with white or black objects. No problem.

More cropping

one parameter used: s6.

If the image to classify is still to big, we must crop a little bit more. We can create a new "cuted" image which contains $s6\%$ ( $s6$ should be 90 or 95) of the luminosity of the original image. The luminosity of an image is defined by the sum of the gray level of all the points in the image.

The "cutting" algorithm is the following:

find the center of gravity of the image (the weight of each point C is weight= $abs(c-128)$ ).
put a box of dimension (1,1) around the center of gravity.
extends this box in the direction which increases the most the weight of the box.
go to point 3 while the luminosity of the box is lower than $s6\%$ of the global luminosity.

Fast features extraction.

four parameters used: s7,s8,s9,s10.

With the toolbox you can easily extract these features (all these in less the 10 ms on a P3 600 MHz):

surface
height
width
aspect ratio
(number of bright pixel)/(number of dark pixel)
lowest gray level
highest gray level
number of peaks in the x direction.
For each column of the image, we calculate the average of the gray level. This average follows a curve $C1$ . To be less sensitive to the noise, we count the number of peaks of the curve $C2$ with $C2(x)=floor(C1(x)/s7)$ .
number of peaks in the y direction.
For each column of the image, we calculate the average of the gray level. This average follows a curve $C1$ . To be less sensitive to the noise, we count the number of peaks of the curve $C2$ with $C2(y)=floor(C1(y)/s8)$ .
number of radial peaks.
For each column of the image, we calculate the average of the gray level. This average follows a curve $C1$ . To be less sensitive to the noise, we count the number of peaks of the curve $C2$ with $C2(r)=floor(C1(r)/s9)$ .
number of angular peaks.
For each column of the image, we calculate the average of the gray level. This average follows a curve $C1$ . To be less sensitive to the noise, we count the number of peaks of the curve $C2$ with $C2(\theta)=floor(C1(\theta)/s10)$ .

Slow feature extraction: image correlations.

The correlation of an image $I1$ of size $(X1,Y1)$ with an image $I2$ of size $(X2,Y2)$ is an image $IC$ of size $(X1,Y1)$
(non-commutativity of the correlation operator).

$\displaystyle IC(x,y)$	$\displaystyle =$	$\displaystyle Corr_{(I1,I2)}(x,y)$	(3)
	$\displaystyle =$	$\displaystyle I1 * (I2)'$	(4)
	$\displaystyle =$	$\displaystyle \sum_{i=1}^{i=X2} \;\; \sum_{j=1}^{j=Y2} \; I1(i+x,j+y) \; I2(i,j)$	(5)

with $x=1,...,X1$ and $y=1,...,Y1$ .
( $I2$ )' is the image $I2$ after a rotation of 180°.
The star * is the convolution operator.
With the convention that $I1(a,b)=0 \;\; \forall (a>X1)$ and $\forall (b>Y1)$ .

The equation 5 is way to slow. We will use an other technique. For the calculation of the correlation between two images of size (128,128), this second technique is more than 100 times faster than direct application of equation 5.

Let's define:

$\displaystyle \mathcal{I}1$	$\displaystyle =$	$\displaystyle \mathcal{F}( I1 )$	(6)
$\displaystyle \mathcal{I}2$	$\displaystyle =$	$\displaystyle \mathcal{F}( I2 )$	(7)
$\displaystyle \mathcal{I}C$	$\displaystyle =$	$\displaystyle \mathcal{F}( IC )$	(8)

with $\mathcal{F}(I)$ the Fourier transform of the image I.
We have:

$\displaystyle IC$	$\displaystyle =$	$\displaystyle I1 * (I2)'$	(9)
$\displaystyle \mathcal{I}C (i,j)$	$\displaystyle =$	$\displaystyle \mathcal{I}1(i,j) \; ( \mathcal{I}2(i,j) )^{*}$	(10)

with $x^{*}$ = transpose of x.

The convolution operator is a simple multiplication in the Fourier domain. For each point, we calculate only a single multiplication.

Now, we have $\mathcal{I}C$ . we want $IC$ . We still have to calculate an inverse Fourier Transform:

$\displaystyle IC = \mathcal{F}^{-1} ( \mathcal{I}C )$

(11)

The Fourier transforms are calculated using an algorithm called FFT: "Fast Fourier Transform". This algorithm imposes that all the dimension of the images are exactly a power of two: 2,4,8,16,32,64,128,256,512,... We will pad (enlarge) the images to have an allowed size (with zero's).

The correlation of two images is available only for images where the gray level is coded on a double ("ImageD" class). There is a simple function which creates "ImageD" images from normal images where the gray level is coded in integer on 8 bits (normal "Image" class).

It's interesting to calculate the correlation of the images that you want to classify with "prototype" images to see "how close they look like". This feature is very slow to calculate but it usually contains lots of useful information. The result of the correlation calculation is an image. From this image, we will only use (as a feature to inject inside a classifier) the greatest value of the color of the pixels of $IC$ .

An example

We have an image 'input.png' with noise on it. We want to know if this image is a duck or a tomato (classification in two classes). We will do a correlation of the input image with one reference image of a duck ('duck.png') and one reference image of a tomato ('tomato.png'). The result of this correlation will be used to determine in with class belong the image 'input.png'.

input.png
(500x350)

duck.png
(80x87)

tomato.png
(100x93)

We will first try to remove the noise using the ceiling technique. We obtain:

'inter0.png'
(500x350)
after ceiling

Everything which was near the "neutral" background gray level 128 has been rounded to 128. We will now isolate the only object of interest in this image (later we will compare this object with the 2 reference objects). We will use a cropping technique.

'inter1.png'
(250x175)
The "flood fill" has covered all the object of interest.
We will only take the part of the image
covered by the flood fill

'inter2.png'
(150x85)
After cropping we have isolated
the object to classify

The size of the image is still too big. A big part of the image is noise. We will apply the second cropping technique

'inter3.png'
(84x82)

We are now ready to start the correlation with the reference images (do not forget to pad the images to a size which is a power of two).

'inter4.png'
(128x128)
'inter3.png' after padding

*

'corr0.png'
(128x128)
'duck.png' after padding

=

'corr1.png'
(128x128)
The correlation of the two previous images

We will now extract from 'corr1.png' the gray level of its best point (brightest point). We divide this value by the surface of the image (128x128) (kind of normalization). We finally obtain 1291,486084. The correlation between the input image 'input.png' and the reference image 'duck.bmp' is thus 1291.486084

'inter4.png'
(128x128)
'inter3.png' after padding

*

'corr2.png'
(128x128)
'tomato.png' after padding

=

'corr3.png'
(128x128)
The correlation of the two previous images

The correlation between the input image 'input.png' and the reference image 'tomato.png' is 4.956055 (value extracted from 'corr3.png').

The final results is that (hopefully) 'input.png' looks more like a duck than a tomato (1291.486084>4.956055).

The whole calculation time for the 2 correlations is lower than 80ms on my P3 600 MHz. Thanks to the FFT algorithm!

An other example

We will calculate the following correlation (click on the images to see them in full,real size):

'inter5.png' (512x512) 'input2.png' after padding	*	'corr4.png' (512x512) 'duck.png' after padding
= (512x512)

Note the two white spot locatted exacly at the position of the duck inside 'input2.png'. The white spot which is beneath is brighter because the 'input2.png' ressemble the most at a duck at this position. The emplacement of the tomato is visible thanks to the black spot.

Calculation time for this correlation is about 3s on my P3 600 MHz.

Download

You can download the full image processing toolbox. This toolbox has been speed-optimized for real-time applications. It has been extensivelly tested in real condition in factory. It is pure C/C++ code which compiles on windows, unix and solaris. It does not requires any special libraries. It is completely stand-alone. The toolbox contains a complete example ('example.cpp') of use. This example generates all the figures seen on this page.

The mathematical part of this page is downloadable here in PDF (unfortunately, it doesn't contains the fun examples).