



Next: Annexes
Up: Conclusions
Previous: Some advice on how
Contents
The
H-norm
The shape of an ideal trust region should reflect the geometry of
the model and not give undeserved weight to certain directions.
Perhaps the ideal trust region would be in the
H-norm,
for which
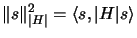 |
(12.3) |
and
where the absolute value 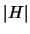 is defined by
is defined by
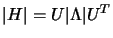 , where
, where 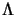 is a diagonal matrix constituted by the
eigenvalues of
is a diagonal matrix constituted by the
eigenvalues of 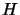 and where
and where 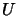 is an orthonormal matrix of the
associated eigenvectors and where the absolute value
is an orthonormal matrix of the
associated eigenvectors and where the absolute value 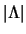 of the diagonal matrix
of the diagonal matrix 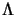 is simply the matrix formed by
taking absolute values of its entries.
is simply the matrix formed by
taking absolute values of its entries.
This norm reflects the proper scaling of the underlying problem -
directions for which the model is changing fastest, and thus
directions for which the model may differ most from the true
function are restricted more than those for which the curvature
is small.
The eigenvalue decomposition is extremely expensive to compute. A
solution, is to consider the less expensive symmetric, indefinite
factorization
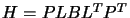 (
(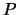 is a permutation matrix,
is a permutation matrix, 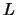 is
unit lower triangular,
is
unit lower triangular, 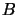 is block diagonal with blocks of size
at most 2). We will use
is block diagonal with blocks of size
at most 2). We will use
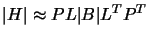 with
with 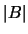 computed by taking the absolute values of the 1 by 1 pivots and by
forming an independent spectral decomposition of each of the 2 by
2 pivots and reversing the signs of any resulting negative
eigenvalues.
computed by taking the absolute values of the 1 by 1 pivots and by
forming an independent spectral decomposition of each of the 2 by
2 pivots and reversing the signs of any resulting negative
eigenvalues.
For more information see [CGT00g].




Next: Annexes
Up: Conclusions
Previous: Some advice on how
Contents
Frank Vanden Berghen
2004-04-19