Document version v1.01
The PDF version of this page is available
here.
The mini-SSE-L1-BLAS Library is providing the basic Level 1 BLAS
operations on vectors. In particular, the four functions: SDOT, DDOT, SAXPY,
DAXPY were deeply hand-optimized. The library is composed of only 2 small files
(a ".cpp" and a ".h" file). Inclusion of the library inside your own projects
is easy. It is cross-platform. It compiles transparently on both Visual Studio
.NET and GCC. A FORTRAN interface is also available. Optimization includes inline
SSE and SSE2 assembly code inserted inside the C/C++ code, loop unrolling. Assembly
code instructions are ordered to increase parallel execution of instructions,
to ease branch prediction, to reduce dependency links between two close instructions.
Software Prefetch instructions were very roughly investigated but were not included
in the library. The functions are also implemented as C++ macros to remove the
function calls overhead.
SDOT and DDOT operations compute dot vector products (
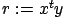 with
with
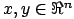 ). SAXPY and DAXPY operations
compute
). SAXPY and DAXPY operations
compute
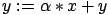 (
(
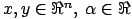 ). The S or D prefix on SDOT,DDOT,SAXPY,DAXPY
operations means that the operations are either performed on float's (S) or
on double's (D).
). The S or D prefix on SDOT,DDOT,SAXPY,DAXPY
operations means that the operations are either performed on float's (S) or
on double's (D).
You can download
here the mini-SSE-L1-BLAS Library (v1.03;July 15,2006).
A complete User's guide for the FORTRAN interface and for the C++ interface
is given respectively in section 1.3
and section 1.4. If you are in a hurry,
you can skip all the other sections and only read the user's guides (sections 1.3 and 1.4)..
This library is currently used inside my linear
identification tool.
The remaining of this section is about the different code optimizations that
were used for the development of the library. Section 1.2
is about experimental benchmark results. The experimental results show that
the computing time can sometime be divided by four compared to a standard C
implementation. The last section (1.5)
gives some references and useful links.
Here is some background details about the different code optimizations that
have been performed:
- As a general rule of thumb, when optimizing code you should never try to
guess the best strategy based on some empirical reasoning. Always validate
your choices using experimental benchmarks results only.
- SSE and SSE2 are a set of assembly-level instructions that allows to compute
4 products of float's or 2 products of double's in, essentially, the same
time as 1 product using the classical set of assembly-level instructions.
This normally leads to a reduction of the computation time for a SDOT or SAXPY
operation to 25% of a non-optimized classical implementation. For a DDOT or
DAXPY operation the computing time should be reduced to 50% . Unfortunately,
the real bottleneck for high performances is memory access. This means that
we cannot usually obtain such good performance but still we can get close
enough.
- Let's consider this small C code:
int i=n;
double s=0.0;
while (i--) s+=a[i]*b[i];
This code computes the dot-product of 2 vectors of length n: a and b. To reduce
computation time you can unroll (8 times) the main loop:
int i=n>>3, j=0, k=n&7;
double s=0.0;
while (i--)
{
s+=a[j ]*b[j ];
s+=a[j+1]*b[j+1];
s+=a[j+2]*b[j+2];
s+=a[j+3]*b[j+3];
s+=a[j+4]*b[j+4];
s+=a[j+5]*b[j+5];
s+=a[j+6]*b[j+6];
s+=a[j+7]*b[j+7];
j+=8;
}
switch(k)
{
case 7: s+=a[j]*b[j]; j++;
case 6: s+=a[j]*b[j]; j++;
case 5: s+=a[j]*b[j]; j++;
case 4: s+=a[j]*b[j]; j++;
case 3: s+=a[j]*b[j]; j++;
case 2: s+=a[j]*b[j]; j++;
case 1: s+=a[j]*b[j]; j++;
}
The second code is faster because it performs the end-of-loop test "if (i==0)"
once every height multiplies.
- Let's consider this small C code (we assume that
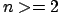 and
and 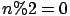 ):
):
int i=0;
register double at,bt,st,s=0.0;
while (i<n)
{
at=a[i ]; bt=b[i ]; st=at*bt; s+=st;
at=a[i+1]; bt=b[i+1]; st=at*bt; s+=st;
i+=2;
}
To reduce computation time you can re-order the instruction inside the main
loop:
int i=0;
register double at,bt,st,s=0.0;
n-=2;
bt=b[i];
while (i<n)
{
at=a[i ]; st=at*bt; bt=b[i+1]; s+=st;
at=a[i+1]; st=at*bt; bt=b[i+3]; s+=st;
i+=2;
}
s+= a[i ] * bt +
a[i+1] * b[i+1];
The second code is faster because it allows parallel execution of instructions.
While the arithmetic-unit of the processor is busy computing "st=at*bt" the
memory-access-unit of the processor can already performs "bt=b[i+1]". This
is called "parallel execution" because the two units are working in parallel.
Unfortunately, in our example, the next instruction (after "bt=b[i+1]") is
"s+=st". To execute this instruction we must wait until the multiplication
"st=at*bt" is finished, loosing some precious time. In other words, there
is a "dependency link" between the instructions "st=at*bt" and "s+=st". We
should re-order the instructions to remove those "dependency link" to increase
parallel execution.
- Let's consider again the unrolled dot product:
int i=n>>3, j=0, k=n&7;
double s=0.0;
while (i--)
{
s+=a[j ]*b[j ];
s+=a[j+1]*b[j+1];
s+=a[j+2]*b[j+2];
s+=a[j+3]*b[j+3];
s+=a[j+4]*b[j+4];
s+=a[j+5]*b[j+5];
s+=a[j+6]*b[j+6];
s+=a[j+7]*b[j+7];
j+=8;
}
switch(k)
{
case 7: s+=a[j]*b[j]; j++;
case 6: s+=a[j]*b[j]; j++;
case 5: s+=a[j]*b[j]; j++;
case 4: s+=a[j]*b[j]; j++;
case 3: s+=a[j]*b[j]; j++;
case 2: s+=a[j]*b[j]; j++;
case 1: s+=a[j]*b[j]; j++;
}
There are different ways to implement this "switch instruction" in assembler:
- CHOICE_1:
k=n&7;
goto JUMP_TABLE[k];
JUMP_TABLE[7]: s+=a[j]*b[j]; j++;
JUMP_TABLE[6]: s+=a[j]*b[j]; j++;
JUMP_TABLE[5]: s+=a[j]*b[j]; j++;
JUMP_TABLE[4]: s+=a[j]*b[j]; j++;
JUMP_TABLE[3]: s+=a[j]*b[j]; j++;
JUMP_TABLE[2]: s+=a[j]*b[j]; j++;
JUMP_TABLE[1]: s+=a[j]*b[j]; j++;
JUMP_TABLE[0]:
Note that the C code used here will not actually compile: It's just to
have a general idea of what is possible in assembler.
- CHOICE_2:
k=n&7;
if (k)
{
s+=a[j]*b[j]; j++; k--;
if (k)
{
s+=a[j]*b[j]; j++; k--;
if (k)
{
s+=a[j]*b[j]; j++; k--;
if (k)
{
s+=a[j]*b[j]; j++; k--;
if (k)
{
s+=a[j]*b[j]; j++; k--;
if (k)
{
s+=a[j]*b[j]; j++; k--;
if (k)
{
s+=a[j]*b[j]; j++;
}
}
}
}
}
}
}
- CHOICE_3:
k=n&7;
if (k)
{
s+=a[j]*b[j];
if (k>3)
{
s+=a[j+1]*b[j+1];
s+=a[j+2]*b[j+2];
s+=a[j+3]*b[j+3];
if (k>5)
{
s+=a[j+4]*b[j+4];
s+=a[j+5]*b[j+5];
if (k==7) s+=a[j+6]*b[j+6];
} else
{
if (k==5) s+=a[j+4]*b[j+4];
}
} else
{
if (k==3)
{
s+=a[j+1]*b[j+1];
s+=a[j+2]*b[j+2];
} else
{
if (k==2)
{
s+=a[j+1]*b[j+1];
}
}
}
j+=k;
}
- CHOICE_4:
k=n&7;
double ss=0.0;
goto JUMP_TABLE[k];
JUMP_TABLE[7]: s +=a[j+6]*b[j+6];
JUMP_TABLE[6]: ss+=a[j+5]*b[j+5];
JUMP_TABLE[5]: s +=a[j+4]*b[j+4];
JUMP_TABLE[4]: ss+=a[j+3]*b[j+3];
JUMP_TABLE[3]: s +=a[j+2]*b[j+2];
JUMP_TABLE[2]: ss+=a[j+1]*b[j+1];
JUMP_TABLE[1]: s +=a[j ]*b[j];
j+=k;
s+=ss;
JUMP_TABLE[0]:
All the compilers will use either CHOICE_1 or CHOICE_2. In particular, CHOICE_1
*seems* very promising because the processor has no test (no "if" instruction)
to perform.
As previously mentioned, the processor is always trying to execute instructions
in parallel. This means that while it is processing the current instruction
it's already preparing and executing instruction "ahead". When the processor
sees a GOTO or JUMP it should be able to guess where it will go using a technique
called "branch prediction". A correct guess allows to prepare "ahead" the
execution of instructions. A wrong guess will cause a major stall in the pipeline
of instructions. Recovering from this pipeline stall is very time-consuming.
CHOICE_3 is superior to CHOICE_2 because it involves less tests. CHOICE_4
is superior to CHOICE_1 because there are less dependency between the instructions.
CHOICE_3 and CHOICE_4 were both implemented. Benchmark results indicates that
CHOICE_3 is the fastest. CHOICE_3 was thus thoroughly used inside the library.
It appears that the only jump performed in CHOICE_4 is harder to predict than
all the small jumps performed in CHOICE_3.
- Variables stored in memory are slow to access. This is why there are two
levels of cache on x86 processors. The following table summarizes the time
required to read data depending on their location:
| Location of Data |
Read time |
| L1 |
< 3 nS |
| L2 |
< 10 nS |
| RAM |
| <100 nS assuming no page page misses plus |
| possible delays to write back a dirty cache line |
|
| Disk |
10+ milliseconds |
| Network Disk |
100 mS to tens of seconds |
The objective of the Prefetch instructions is to load in advance some data
in the L1 or L2 cache to decrease the time needed later to read these data.
The Prefetch instruction takes as parameter a memory address. The data at
this address are copied into the cache. This parameter is difficult to tune.
Some preliminary results show that the usage of the Prefetch instruction inside
the SDOT, DDOT, SAXPY, DAXPY functions did not lead to any speed increase
(on the constrary). I think that more tuning of the Prefetch parameters should
be performed. Prefetch instructions are thus currently not used.
Experimental results
All the tests were performed on the same computer: an INTEL CENTRINO 1.7 GHz with
1GB RAM (DELL inspiron 8600).
All the code optimizations were validated against other strategies using the test
benchmark described in this section.
Table 1 displays the time needed (in milliseconds), to process 5000000 calls to
the SDOT, DDOT, SAXPY, DAXPY functions on vectors of dimension 200. The vectors
are filled with random numbers in
[-500 500]. The percentage in the last column shows the relative time compared
to the time of the first column.
| function |
| Standard C code |
| compiled with |
| MVS.NET |
|
| Standard C code |
| compiled with |
| Intel compiler 7.1 |
| on Windows XP |
|
| Standard C code |
| compiled with |
| GCC_3.4 |
| on Linux |
|
|
| SDOT |
2984 |
3217 |
2964 |
867 |
(29.05 %) |
| DDOT |
2938 |
3130 |
2963 |
1501 |
(51.09 %) |
| SAXPY |
2626 |
3192 |
3305 |
929 |
(35.38 %) |
| DAXPY |
2666 |
3173 |
3290 |
1484 |
(55.66 %) |
Table 1: Timing results (vector dimension=200; 5000000 calls)
The speed of the library is independent of the compiler and of the operating system
since it's written directly in assembler. This is why the performance of the library
is reported only once for all compilers and operating systems.
On this special benchmark, The INTEL compiler and the GCC meta-compiler are slower
than the Visual Studio .NET compiler. Indeed the assembly code generated by the
Visual Studio .NET compiler is from far cleaner than the other assembly code generated
by the other compilers.
The SDOT and DDOT functions are close to the theoretical lower boundary of, respectively,
25 % and 50% of running time compared to the standard C implementation. The SAXPY
and DAXPY functions are a little bit slower than the SDOT and DDOT functions because
they are accessing memory more heavily. Table 2 shows other results with larger
vector dimensions.
| function |
| Standard C code |
| compiled with |
| MVS.NET |
|
| Standard C code |
| compiled with |
| Intel compiler 7.1 |
| on Windows XP |
|
| Standard C code |
| compiled with |
| GCC_3.4 |
| on Linux |
|
|
| SDOT |
2480 |
2823 |
2683 |
947 |
(38.19 %) |
| DDOT |
2549 |
2784 |
2759 |
1896 |
(74.38 %) |
| SAXPY |
2425 |
2707 |
2888 |
1120 |
(46.19 %) |
| DAXPY |
2826 |
2965 |
3054 |
2255 |
(79.79 %) |
Table 2: Timing results (vector dimension=20000; 50000 calls)
Table 2 indicates that, for larger vector sizes, the memory bottleneck becomes
more prominent. Obviously, a correct Prefechtching should help in this case.
The standard C code implementation of SDOT,DDOT,SAXPY,DAXPY that is used in the
experimental results is:
double ddot_C(int n, double *x,double *y)
{ double s=0.0; while (n--) { s+=*(x++) * *(y++); }; return s; }
float sdot_C(int n, float *x,float *y)
{ float s=0.0; while (n--) { s+=*(x++) * *(y++); }; return s; }
void saxpy_C(int n, float a,float *x, float *y)
{ while (n--) *(x++)+= a * *(y++); }
void daxpy_C(int n, double a,double *x, double *y)
{ while (n--) *(x++)+= a * *(y++); }
User's guide for the FORTRAN interface to the library
There is one example inside the ZIP file that demonstrates the usage of the FORTRAN
interface to the library. The example is for a UNIX fortran compiler (f77/g77)
and is makefile-based. The miniSSEL1BLAS library is composed by only two files:
miniSSEL1BLAS.cpp and miniSSEL1BLAS.h. Basically, to use the
library in your own project, you must generate an object file "miniSSEL1BLAS.o"
using the command:
g++ -O -c miniSSEL1BLAS.cpp
Thereafter, you can simply add the object file " miniSSEL1BLAS.o" to
the list of FORTRAN ".f" file that are inside your project. Usually,
you obtain something like:
f77 -o <name_of_the_executable> <list_of_fortran_.f_files> miniSSEL1BLAS.o
The FORTRAN interface implements the following FORTRAN functions:
integer function hasSSE() // out=1 if SSE supported, out=0 otherwise
integer function hasSSE2() // out=1 if SSE2 supported, out=0 otherwise
subroutine scopy (n, sx,sy) // y[i]=x[i] for_all_i
subroutine dcopy (n, dx,dy)
subroutine saxpy (n,sa,sx,sy) // y[i]=a*x[i]+y[i] for_all_i
subroutine saxpyUA (n,sa,sx,sy)
subroutine daxpy (n,da,dx,dy)
subroutine daxpyUA (n,da,dx,dy)
subroutine sscale (n,sa,sx) // x[i]=a*x[i] for_all_i
subroutine dscale (n,da,dx)
subroutine sscaleUA (n,sa,sx)
subroutine dscaleUA (n,da,dx)
real function sdot (n, sx,sy) // out = sum_over_i x[i]*y[i]
real function sdotUA (n, sx,sy)
double precision function ddot (n, dx,dy)
double precision function ddotUA (n, dx,dy)
real function ssquare (n, sx) // out = sum_over_i x[i]**2
real function ssquareUA(n, sx)
double precision function dsquare (n, dx)
double precision function dsquareUA(n, dx)
real function snrm2 (n, sx) // out = sqrt(square(n,x)/n)
real function snrm2UA (n, sx)
double precision function dnrm2 (n, dx)
double precision function dnrm2UA (n, dx)
real function sasum (n, sx) // out = sum_over_i fabs(x[i])
real function sasumUA (n, sx)
double precision function dasum (n, dx)
double precision function dasumUA (n, dx)
real function smin (n, sx) // out = min_for_all_i x[i]
real function sminUA (n, sx)
double precision function dmin (n, dx)
double precision function dminUA (n, dx)
real function smax (n, sx) // out = max_for_all_i x[i]
real function smaxUA (n, sx)
double precision function dmax (n, dx)
double precision function dmaxUA (n, dx)
subroutine sswap (n, sx,sy) // SWAP(x[i],y[i]) for_all_i
subroutine dswap (n, dx,dy)
subroutine sset (n,sa,sx) // x[i]=a for_all_i
subroutine dset (n,da,dx)
The data type of the arguments are:
integer n
real sx(*),sy(*),sa,sc,ss
double precision dx(*),dy(*),da,dc,ds
Six additional functions/subroutines are provided in order to meet the L1 BLAS
requirements. WARNING: these functions are NOT optimized and are thus relatively
slow:
integer function suiamax( n,sx) // out = index i of the maximum of fabs(x[i])
integer function duiamax( n,dx)
subroutine srot (sx,sy,sc,ss) // apply a 2D rotation(c,s) on all the 2D points (x[i],[i])
subroutine drot (dx,dy,dc,ds)
subroutine srotg (sa,sb,sc,ss) // compute a 2D rotation
subroutine drotg (da,db,dc,ds)
The data type of the arguments are:
integer n
real sx(*),sy(*)sa,sb,sc,ss
double precision dx(*),dy(*),da,db,dc,ds
Before using the Level 1 BLAS functions, you should check if the SSE set (or SSE2
set) of instructions is supported by your processor. The library provides the
function "hasSSE" (and the function "hasSSE2") that returns
one if SSE (respectively SSE2) is suppported. Operations in single precision require
SSE support only. Operations in double precision require SSE2 support.
All the vector arrays given as parameters to the LEVEL 1 BLAS FUNCTIONS must start
on a memory address that is a multiple of 16 (this is called 16-byte alignment).
By default, fortran compilers (g77) always allocates arrays with correct alignment.
This means that you can easily do:
int offset,i,n
real sx(100), sy(100), sr
double precision dx(100), dy(100), dr
sr=sdot(n,sx,sy)
dr=ddot(n,dx,dy)
However, the next example will work only if ((offset-1)%4)=0
( The "%" stands for the modulo operation):
sdot(n,sx(offset),sy(offset+i*4))
The next example will only work if ((offset-1)%2)=0 :
ddot(n,dx(offset),dy(offset+i*2))
If you need to work on UnAligned arrays, you can use the LEVEL 1 BLAS FUNCTIONS
that have the UA suffix. The UA suffix inside the name of the
function stands for "UnAligned" memory address. The UA version of the
function is slower but the vector arrays parameters can be un-aligned. However
the un-alignement must be the same for x and for y. In other
word, the following example works for any value of the variable "offset":
int offset,i,n
real s(*)
double precision d(*)
sdotUA(n,s(offset),s(offset+i*4))
ddotUA(n,d(offset),d(offset+i*2))
The functions scopy, dcopy, sswap, dswap, sset, dset, suiamax, duiamax, srot,
drot, srotg, drotg have no UnAligned equivalent. The vector array parameters
given to these functions can be UnAligned.
User's guide for the C++ interface to the library
The library is composed by two files: miniSSEL1BLAS.cpp and miniSSEL1BLAS.h.
These are the only 2 files that you need to include into your own projects to
be able to use the library.
There are two examples to demonstrate the usage of the C++ interface to the library:
- a Visual Studio .NET example (.sln)
- a GCC example (makefile based)
The examples are the benchmarks used in section 1.2.
Before using the Level1 BLAS functions, you should check if the SSE set (or SSE2
set) of instructions is supported by your processor. The library provides the
global boolean variable " hasSSE" (and the global variable "hasSSE2")
that is true if SSE (respectively SSE2) is supported. Operations on float require
SSE support only. Operations on double require SSE2 support.
All the vector arrays given as parameters to the LEVEL 1 BLAS FUNCTIONS must start
on a memory address that is a multiple of 16 (this is called 16-byte alignment).
When using the classical C "malloc" function, only a 8-byte alignment
is assured. You must use the following memory allocations functions to be assured
of correct alignment (these functions are part of the miniSSEL1BLAS library):
void *mallocAligned(unsigned long n); // malloc aligned on 16 byte boundaries
void freeAligned(void *t); // free the aligned allocation
Let's consider this small C code:
int i= ...any number...
float *f=(float*)mallocAligned(...any number...),
*fA=f+i*4;
double *d=(double*)mallocAligned(...any number...),
*dA=d+i*2;
You can use the vector arrays f,fA,d,dA inside the Level1 BLAS functions because
all these arrays are correctly aligned.
The LEVEL 1 BLAS functions are available as standard C++ functions as defined
below.
float dot (int n, float *x, float *y); // out = sum_over_i x[i]*y[i]
double dot (int n, double *x, double *y);
void axpy (int n, float a, float *x, float *y); // y[i]+=a*x[i] for_all_i
void axpy (int n, double a, double *x, double *y);
void vcopy (int n, float *x, float *y); // y[i]=x[i] for_all_i
void vcopy (int n, double *x, double *y);
void vscale (int n, float a, float *x); // x[i]*=a for_all_i
void vscale (int n, double a, double *x);
float asum (int n, float *x); // out = sum_over_i fabs(x[i])
double asum (int n, double *x);
float square (int n, float *x); // out = sum_over_i x[i]**2
double square (int n, double *x);
float nrm2 (int n, float *x); // out = sqrt(square(n,x)/n)
double nrm2 (int n, double *x);
float vmin (int n, float *x); // out = min_for_all_i x[i]
double vmin (int n, double *x);
float vmax (int n, float *x); // out = max_for_all_i x[i]
double vmax (int n, double *x);
void vswap (int n, float *x, float *y); // SWAP(x[i],y[i]) for_all_i
void vswap (int n, double *x, double *y);
void vset (int n, float a, float *x); // x[i]=a for_all_i
void vset (int n, double a, double *x);
Six additional functions/subroutines are provided in order to meet the L1 BLAS
requirements. WARNING: these functions are NOT optimized and thus are relatively
slow:
int uiamax(int n, double *x); // out = index i of the maximum of fabs(x[i])
int uiamax(int n, float *x);
void rot (int *n, float *x, float *y, float c,float s); // apply a 2D rotation(c,s) on all the 2D points (x[i],[i])
void rot (int *n, double *x, double *y, double c,double s);
void rotg ( float *a, float *b, float *c,float *s); // compute a 2D rotation
void rotg ( double *a, double *b, double *c,double *s);
The usage is straightforward as soon as the vector arrays x and y
are correctly aligned. If the arrays x and y are not correctly
aligned, you can still use:
float dotUA (int n, float *x, float *y);
double dotUA (int n, double *x, double *y);
void axpyUA (int n, float a, float *x, float *y);
void axpyUA (int n, double a, double *x, double *y);
void vscaleUA(int n, float a, float *x);
void vscaleUA(int n, double a, double *x);
float asumUA (int n, float *x);
double asumUA (int n, double *x);
float squareUA(int n, float *x);
double squareUA(int n, double *x);
float nrm2UA (int n, float *x);
double nrm2UA (int n, double *x);
float vminUA (int n, float *x);
double vminUA (int n, double *x);
float vmaxUA (int n, float *x);
double vmaxUA (int n, double *x);
The suffix "UA" stands for "Un-Aligned". The UnAligned versions of the
functions is slower. Furthermore, the un-alignement must be the same for x
and for y: We must have (x%16)=(y%16). The
"%" sign is the modulo operator. In other words, we can have:
int i;
float *f=(float *)malloc(...); // f is not aligned
double *d=(double*)malloc(...); // d is not aligned
...
sdotUA(n,f,f+i*4); // f is not aligned
ddotUA(n,d,d+i*2); // d is not aligned
In opposition, we cannot have:
sdot(n,f,f+i*4); // f is not aligned
ddot(n,d,d+i*2); // d is not aligned
The functions vcopy, vswap, vset, uiamax, rot, rotg have no UnAligned
equivalent. The vector array parameters given to these functions can be UnAligned.
Some LEVEL 1 BLAS functions are also available as C++ MACRO's:
unsigned int n;
float *xf,*yf,af,rf; // xf,yf are correctly aligned.
double *xd,*yd,ad,rd; // xd,yd are correctly aligned.
SDOT_SSE (A,n, xf,yf,rf) // rf = sum_over_i xf[i]*yf[i]
DDOT_SSE2(A,n, xd,yd,rd) // rd = sum_over_i xd[i]*yd[i]
SAXPY_SSE (A,n,af,xf,yf) // yf[i]+=af*xf[i] for_all_i
DAXPY_SSE2(A,n,ad,xd,yd) // yd[i]+=ad*xd[i] for_all_i
SSCALE_SSE (A,n,af,xf) // xf[i]*=af for_all_i
DSCALE_SSE2(A,n,ad,xd) // xd[i]*=ad for_all_i
SSQUARE_SSE (A,n, xf,rf) // rf = sum_over_i xf[i]**2
DSQUARE_SSE2(A,n, xd,rd) // rd = sum_over_i xd[i]**2
SASUM_SSE (A,n, xd,rd) // rf = sum_over_i fabs(xf[i])
DASUM_SSE2(A,n, xf,rd) // rd = sum_over_i fabs(xd[i])
SMIN_SSE (A,n, xf,rf) // rf = min_for_all_i xf[i]
DMIN_SSE2(A,n, xd,rd) // rd = min_for_all_i xd[i]
SMAX_SSE (A,n, xf,rf) // rf = max_for_all_i xf[i]
DMAX_SSE2(A,n, xd,rd) // rd = max_for_all_i xd[i]
float *xfu,*yfu,af; // xfu,yfu can be Un-Aligned.
double *xdu, ,ad; // xdu can be Un-Aligned.
MEMSWAP_MMX (A,n, xfu,yfu) // SWAP(xf[i],yf[i]) for_all_i
SMEMSET_MMX (A,n,af,xfu) // xf[i]=af for_all_i
DMEMSET_MMX (A,n,ad,xdu) // xd[i]=ad for_all_i
The arguments given to the MACRO's must exactly be of the type specified above.
The vector arrays xf,yf,xd,yd must be correctly aligned. Let's now look
at the first argument (in the examples above, it's "A"). If you try to
compile the following code, the compiler will complain about multiple definition
of the same symbols:
...
float *x1,*y1,r1,
*x2,*y2,r2;
...
SDOT_SSE(A,n,x1,y1,r1);
SDOT_SSE(A,n,x2,y2,r2);
...
The following code compiles without any problem:
...
SDOT_SSE(A,n,x1,y1,r1);
SDOT_SSE(B,n,x2,y2,r2);
...
The first argument of the MACRO must be different at each inclusion of the MACRO
inside the same file. As you can see, the usage of the MACRO version of the functions
is slightly more complex. On the other hand, you can remove all the function call
overheads that are quite time-consuming on big loops.
What processor can I use?
All the functions (except vcopy, vset and vswap) are using either SSE or SSE2
intructions. Operations on floats are performed using SSE instruction sets only.
Operations on doubles are performed using SSE2 instructions.
SSE support is included in:
- Intel® Pentium III and above
- AMD's 3Dnow!™ Professional technology, which is supported in
- AMD Athlon XP
- AMD Athlon MP
- mobile AMD Athlon 4
- Model 7 AMD Duron™ processors.
- AMD opteron, AMD Athlon 64 and above
The oldest AMD processor supporting SSE is an AMD Athlon XP 1500+ at a frequency
of 1333 MHz.
SSE2 support is included in:
- Intel® Pentium 4, Intel® Pentium M
- AMD opteron, AMD Athlon 64 and above
References
To have some good guidelines on how to write optimized loops containing conditional
branches, see the article about the D-loop pattern. I really think that every
programmer can gain some clever insight through this article. That's a must-read!
The article is available here.
A local copy of the article is here: d-loop.pdf
The famous BLAS library: BLAS (Basic Linear Algebra Subprograms): http://www.netlib.org/blas/
Quick-Reference to all the BLAS functions: blasqr.pdf.
Here are some "improved version" of the standard BLAS library:
Some good overall information on MMX/SSE/SSE2 technology:
Some information about Prefetching for x86:
- James Mc Parlane's Blog: x86 Cache Prefetch:
- Memory Access is the Key To Speed (The table about access time for the different
kind of memory is coming from this site).
Some part of the miniSSEL1BLAS library is inspired by code found in the GnuRadio:
http://www.gnu.org/software/gnuradio/
These guys know how to code!
I am usually coding in assembler using Intel MASM style. To know how to convert
MASM style assembler code to GCC-gnu style, see Brennan's Guide to Inline GNU
Assembly: http://www.delorie.com/djgpp/doc/brennan/brennan_att_inline_djgpp.html
(local copy here).
Assembler implementation of a very efficient memcpy
function.
Some information about binary storage inside memory of floating point numbers:
float-ieee754.pdf