


Next: Formal description
Up: Introduction
Previous: Introduction
Contents
We find very often in the industry simulators of huge chemical reactors, simulators
of huge turbo-compressors, simulators of the path of a satellite in low orbit
around earth,... These simulators were written to allow the design engineer to
correctly estimate the consequences of the adjustment of one (or many) design
variables (or parameters of the problem). Such codes very often demands a great
deal of computing power. One run of the simulator can take as much as one or two
hours to finish. Some extreme simulations take a day to complete.
These kinds of code can be used to optimize ``in batch'' the design variables:
The research engineer can aggregate the results of the simulation in one unique
number which represents the ``goodness'' of the current design. This final number
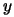 can be seen as the result of the evaluation of an objective function
can be seen as the result of the evaluation of an objective function
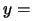
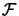
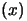 where
where 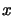 is the vector of design variables and
is the vector of design variables and
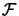 is the simulator. We can run an optimization program
which find
is the simulator. We can run an optimization program
which find 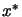 , the optimum of
, the optimum of
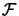
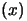 .
.
Most optimization algorithms require the derivatives of
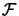
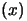 to be available. Unfortunately, we usually don't have them. Very
often, there is also some noises on
to be available. Unfortunately, we usually don't have them. Very
often, there is also some noises on
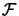
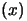 due to rounding errors. To overcome these limitations, I present
here a new optimizer called ``CONDOR''.
due to rounding errors. To overcome these limitations, I present
here a new optimizer called ``CONDOR''.
Here are the assumptions needed to use this new optimizer:
- The dimension
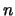 of the search space must be lower than 50.
For larger dimension the time consumed by this algorithm will be
so long and the number of function evaluations will be so huge
that I don't advice you to use it.
of the search space must be lower than 50.
For larger dimension the time consumed by this algorithm will be
so long and the number of function evaluations will be so huge
that I don't advice you to use it.
- No derivatives of
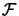
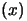 are required. However, the
algorithm assumes that they exists. If the function is not
continuous, the algorithm can still converge but in a greater
time.
are required. However, the
algorithm assumes that they exists. If the function is not
continuous, the algorithm can still converge but in a greater
time.
- The algorithm tries to minimize the number of evaluations of
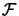
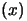 , at the cost of a huge amount of routine work that occurs
during the decision of the next value of
, at the cost of a huge amount of routine work that occurs
during the decision of the next value of 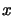 to try. Therefore,
the algorithm is particularly well suited for high computing load
objective function.
to try. Therefore,
the algorithm is particularly well suited for high computing load
objective function.
- The algorithm will only find a local minimum of
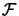
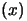 .
.
- There can be a limited noise on the evaluation of
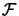
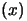 .
.
- All the design variables must be continuous.
- The non-linear constraints are ``cheap'' to evaluate.



Next: Formal description
Up: Introduction
Previous: Introduction
Contents
Frank Vanden Berghen
2004-04-19