Contents

• Summary
• Acknowledgments - Remerciements
  
  
• Introduction
  • Motivations
  • Formal description
  
  
• Unconstrained Optimization
  • An introduction to the CONDOR algorithm.
    • Trust Region and Line-search Methods.
      • Conventions
      • General principle
      • Notion of Speed of convergence.
      • A simple line-search method: The Newton's method.
      • $B_k$ must be positive definite for Line-search methods.
      • Why is Newton's method crucial: Dennis-Moré theorem
    • A simple trust-region algorithm.
    • The basic trust-region algorithm (BTR).
    • About the CONDOR algorithm.
  • Multivariate Lagrange Interpolation
    • Introduction
    • A small reminder about univariate interpolation.
      • Lagrange interpolation
      • Newton interpolation
      • The divided difference for the Newton form.
      • The Horner scheme
    • Multivariate Lagrange interpolation.
      • The Lagrange polynomial basis $\{P_1(x), \ldots , P_N(x)\}$.
      • The Lagrange interpolation polynomial $L(x)$.
      • The multivariate Horner scheme
    • The Lagrange Interpolation inside the optimization loop.
      • A bound on the interpolation error.
      • Validity of the interpolation in a radius of $\rho$ around $\boldsymbol {x}_{(k)}$.
      • Find a good point to replace in the interpolation.
      • Replace the interpolation point $\boldsymbol {x}_{(t)}$ by a new point $X$.
      • Generation of the first set of point $\{ \boldsymbol {x}_{(1)}, \ldots , \boldsymbol {x}_{(N)} \}$.
      • Translation of a polynomial.
  • The Trust-Region subproblem
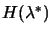    • $H(\lambda ^*)$ must be positive definite.
    • Explanation of the Hard case.
      • Convex example.
      • Non-Convex example.
      • The hard case.
    • Finding the root of $\Vert s(\lambda) \Vert _2 - \Delta =0$.
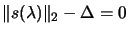    • Starting and safe-guarding Newton's method
    • How to pick 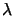$\lambda$ inside $[\lambda _L \lambda _U]$ ?
    • Initial values of 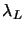$\lambda _L$ and $\lambda _U$
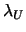
    • How to find a good approximation of 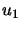$u_1$ : LINPACK METHOD
    • The Rayleigh quotient trick
    • Termination Test.
      • $s(\lambda )$ is near the boundary of the trust region: normal case
      • $s(\lambda )$ is inside the trust region: hard case
    • An estimation of the slope of 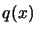$q(x)$ at the origin.
  • The secondary Trust-Region subproblem
    • Generating $\tilde{s}$.
    • Generating $\hat{u}$ and $\tilde{u}$ from $\hat{s}$ and $\tilde{s}$
    • Generating the final $s$ from $\hat{u}$ and $\tilde{u}$.
    • About the choice of $\tilde{s}$
  • The CONDOR unconstrained algorithm.
    • The bound $\epsilon$.
    • Note about the validity check.
    • The parallel extension of CONDOR
  • Numerical Results of CONDOR.
    • Random objective functions
    • Hock and Schittkowski set
    • Parallel results on the Hock and Schittkowski set
    • Noisy optimization
  
  
• Constrained Optimization
  • A short review of the available techniques.
    • Linear constraints
      • Active set - Null space method
      • Gradient Projection Methods
    • Non-Linear constraints
      • Penalty Methods
      • Barrier Methods
    • Primal-dual interior point
      • Duality
      • A primal-dual Algorithm
      • Central path
      • Link between Barrier method and Interior point method
      • A final note on primal-dual algorithms.
      • SQP Methods
      • A small note about the H matrix in the SQP algorithm.
      • A final note about the SQP algorithm.
    • The final choice of a constrained algorithm
  • Detailed description of the constrained step
    • The QP algorithm
      • Equality constraints
      • Active Set methods
      • Duality in QP programming
      • A note on the implemented QP
    • The SQP algorithm
      • Length of the step.
      • Maratos effect: The SOC step.
      • Update of $H_k$
      • Stopping condition
      • The SQP in detail
    • The constrained step in detail
    • Remarks about the constrained step.
  • Numerical Results for the constrained algorithm
  • The METHOD project
    • Parametrization of the shape of the blades
    • Preliminary research
    • Preliminary numerical results
    • Interface between CONDOR and XFLOS / Pre-Solve phase
      • Config file on client node
  • Conclusions
    • About the code
    • Improvements
      • Unconstrained case
      • Constrained case
    • Some advice on how to use the code.
    • The H-norm
  • Annexes
    • Line-Search addenda.
      • Speed of convergence of Newton's method.
      • How to improve Newton's method : Zoutendijk Theorem.
    • Gram-Schmidt orthogonalization procedure.
    • Notions of constrained optimization
    • The secant equation
    • 1D Newton's search
    • Newton's method for non-linear equations
    • Cholesky decomposition.
      • Performing $LU$ decomposition.
      • Performing Cholesky decomposition.
    • QR factorization
    • A simple direct optimizer: the Rosenbrock optimizer
  • Code
    • Rosenbrock's optimizer
      • rosenbrock.cpp
      • rosenbrock.h
      • testR1.cpp
    • AMPL files
      • hs022
      • hs023
      • hs026
      • hs034
      • hs038
      • hs044
      • hs065
      • hs076
      • hs100
      • hs106
      • hs108
      • hs116
      • hs268
  
  
• Bibliography
• About this document ...