



Next: A simple direct optimizer:
Up: Annexes
Previous: Cholesky decomposition.
Contents
There is another matrix factorization that is sometimes very
useful, the so-called QR decomposition,
![$\displaystyle A = Q \left[
\begin{array}{c} R \\ 0 \end{array} \right] \;\;\;...
...n
\Re^{m \times n} (m \geq n), Q \in \Re^{m \times m}, R \in \Re^{n
\times n}$](img1450.png) |
(13.44) |
Here 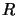 is upper triangular, while
is upper triangular, while 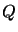 is
orthogonal, that is,
is
orthogonal, that is,
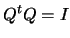 |
(13.45) |
where 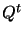 is the transpose
matrix of
is the transpose
matrix of 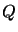 . The standard algorithm for the QR decomposition
involves successive Householder transformations. The Householder
algorithm reduces a matrix A to the triangular form R by
. The standard algorithm for the QR decomposition
involves successive Householder transformations. The Householder
algorithm reduces a matrix A to the triangular form R by 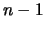 orthogonal transformations. An appropriate Householder matrix
applied to a given matrix can zero all elements in a column of the
matrix situated below a chosen element. Thus we arrange for the
first Householder matrix
orthogonal transformations. An appropriate Householder matrix
applied to a given matrix can zero all elements in a column of the
matrix situated below a chosen element. Thus we arrange for the
first Householder matrix 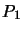 to zero all elements in the first
column of
to zero all elements in the first
column of 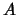 below the first element. Similarly
below the first element. Similarly 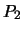 zeroes all
elements in the second column below the second element, and so on
up to
zeroes all
elements in the second column below the second element, and so on
up to 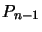 . The Householder matrix
. The Householder matrix 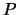 has the form:
has the form:
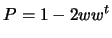 |
(13.46) |
where 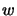 is a real vector with
is a real vector with
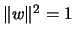 . The
matrix
. The
matrix 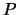 is orthogonal, because
is orthogonal, because
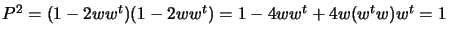 . Therefore
. Therefore
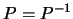 .
But
.
But 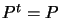 , and so
, and so
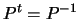 , proving orthogonality.
Let's rewrite
, proving orthogonality.
Let's rewrite 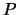 as
as
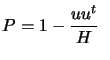 with with
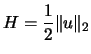 |
(13.47) |
and 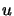 can now be any vector.
Suppose
can now be any vector.
Suppose 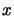 is the vector composed of the first column of
is the vector composed of the first column of 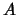 .
Choose
.
Choose
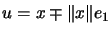 where
where 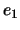 is the unit vector
is the unit vector
![$ [1,0,
\ldots, 0]^t$](img1467.png) , and the choice of signs will be made later. Then
, and the choice of signs will be made later. Then
This shows that the Householder matrix P
acts on a given vector 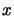 to zero all its elements except the
first one. To reduce a symmetric matrix
to zero all its elements except the
first one. To reduce a symmetric matrix 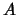 to triangular form, we
choose the vector
to triangular form, we
choose the vector 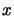 for the first Householder matrix to be the
first column. Then the lower
for the first Householder matrix to be the
first column. Then the lower 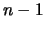 elements will be zeroed:
elements will be zeroed:
![$\displaystyle P_1 A = A'= \left[ \begin{array}{c\vert c} a'_{11} & \\ 0 & \\ \vdots &
\raisebox{.5cm}{\em irrelevant} \\ 0 &
\end{array} \right]$](img1473.png) |
(13.48) |
If the vector 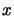 for the second Householder matrix is the lower
for the second Householder matrix is the lower
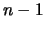 elements of the second column, then the lower
elements of the second column, then the lower 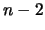 elements
will be zeroed:
elements
will be zeroed:
![$\displaystyle \left[ \begin{array}{c\vert c} 1 & 0
\ldots 0 \\ \hline 0 & \\ ...
...ts & \vdots & \raisebox{.5cm}{\em irrelevant}
\\ 0 & 0 &
\end{array} \right]$](img1475.png) |
(13.49) |
Where
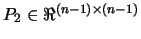 and
the quantity
and
the quantity 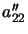 is simply plus or minus the magnitude of
the vector
is simply plus or minus the magnitude of
the vector
![$ [\; a'_{22} \; \cdots \; a'_{n2} \; ]^t $](img1478.png) . Clearly a
sequence of
. Clearly a
sequence of 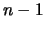 such transformation will reduce the matrix A to
triangular form
such transformation will reduce the matrix A to
triangular form 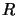 . Instead of actually carrying out the matrix
multiplications in
. Instead of actually carrying out the matrix
multiplications in 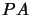 , we compute a vector
, we compute a vector
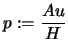 . Then
. Then
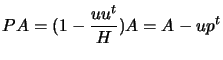 . This is a computationally useful formula. We have the
following:
. This is a computationally useful formula. We have the
following:
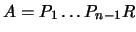 . We will thus form
. We will thus form
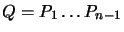 by recursion after all the
by recursion after all the 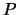 's have been
determined:
's have been
determined:
No extra storage is needed for intermediate
results but the original matrix is destroyed.




Next: A simple direct optimizer:
Up: Annexes
Previous: Cholesky decomposition.
Contents
Frank Vanden Berghen
2004-04-19
![$\displaystyle A = Q \left[
\begin{array}{c} R \\ 0 \end{array} \right] \;\;\;...
...n
\Re^{m \times n} (m \geq n), Q \in \Re^{m \times m}, R \in \Re^{n
\times n}$](img1450.png)
![$\displaystyle A = Q \left[
\begin{array}{c} R \\ 0 \end{array} \right] \;\;\;...
...n
\Re^{m \times n} (m \geq n), Q \in \Re^{m \times m}, R \in \Re^{n
\times n}$](img1450.png)
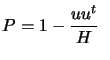 with
with
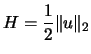
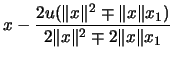
![$\displaystyle P_1 A = A'= \left[ \begin{array}{c\vert c} a'_{11} & \\ 0 & \\ \vdots &
\raisebox{.5cm}{\em irrelevant} \\ 0 &
\end{array} \right]$](img1473.png)
![$\displaystyle \left[ \begin{array}{c\vert c} 1 & 0
\ldots 0 \\ \hline 0 & \\ ...
...ts & \vdots & \raisebox{.5cm}{\em irrelevant}
\\ 0 & 0 &
\end{array} \right]$](img1475.png)
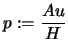 . Then
. Then
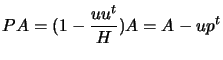 . This is a computationally useful formula. We have the
following:
. This is a computationally useful formula. We have the
following: