



Next: QR factorization
Up: Annexes
Previous: Newton's method for non-linear
Contents
Subsections
Cholesky decomposition.
The Cholesky decomposition can be applied on any square matrix 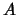 which is symmetric and positive definite. The Cholesky
decomposition is one of the fastest decomposition available. It
constructs a lower triangular matrix L which has the following
property:
which is symmetric and positive definite. The Cholesky
decomposition is one of the fastest decomposition available. It
constructs a lower triangular matrix L which has the following
property:
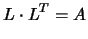 |
(13.33) |
This factorization is sometimes
referred to, as ``taking the square root'' of the matrix 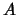 .
.
The Cholesky decomposition is a particular case of the 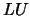 decomposition. The
decomposition. The 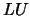 decomposition is the following:
decomposition is the following:
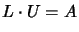 |
(13.34) |
where 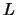 is a lower triangular
matrix and
is a lower triangular
matrix and 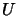 is a upper triangular matrix. For example, in the
case of a
is a upper triangular matrix. For example, in the
case of a
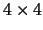 matrix
matrix 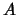 , we have:
, we have:
 |
(13.35) |
We can use the 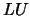 decomposition to solve the linear set:
decomposition to solve the linear set:
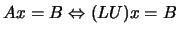 by first solving for the vector
by first solving for the vector 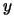 such
that
such
that 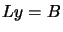 and then solving
and then solving 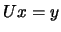 . These two systems are trivial
to solve because they are triangular.
. These two systems are trivial
to solve because they are triangular.
First let us rewrite the component 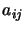 of
of 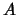 from the
equation 13.34 or 13.35. That component is always a
sum beginning with
The number of terms in the sum depends, however on wether
from the
equation 13.34 or 13.35. That component is always a
sum beginning with
The number of terms in the sum depends, however on wether 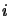 or
or 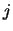 is the smallest number. We have, in fact three cases:
is the smallest number. We have, in fact three cases:
Equations 13.36 - 13.38, totalize 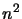 equations
for the
equations
for the 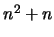 unknown
unknown 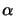 's and
's and 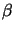 's (the diagonal
being represented twice). Since the number of unknowns is greater
than the number of equations, we have to specify
's (the diagonal
being represented twice). Since the number of unknowns is greater
than the number of equations, we have to specify 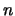 of the
unknowns arbitrarily and then solve for the others. In fact, as we
shall see, it is always possible to take:
of the
unknowns arbitrarily and then solve for the others. In fact, as we
shall see, it is always possible to take:
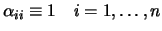 |
(13.39) |
A surprising procedure,
now, is Crout's algorithm, which, quite trivially, solves
the set of 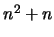 Equations 13.36 - 13.38 for all
the
Equations 13.36 - 13.38 for all
the 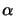 's and
's and 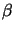 's by just arranging the equation in a
certain order! That order is as follows:
If you work through a few iterations of the above procedure, you
will see that the
's by just arranging the equation in a
certain order! That order is as follows:
If you work through a few iterations of the above procedure, you
will see that the 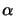 's and
's and 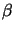 's that occur on the
right-hand side of the Equation 13.40 and 13.41 are
already determined by the time they are needed.
's that occur on the
right-hand side of the Equation 13.40 and 13.41 are
already determined by the time they are needed.
We can obtain the analogs of Equations 13.40 and
13.41 for the Cholesky decomposition:
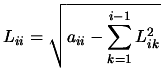 |
(13.42) |
and
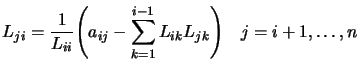 |
(13.43) |
If you apply Equation 13.42 and 13.43 in the order
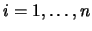 , you will see the the
, you will see the the 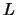 's that occur on the
right-hand side are exactly determined by the time they are
needed. Also, only components
's that occur on the
right-hand side are exactly determined by the time they are
needed. Also, only components 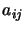 with
with 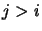 are
referenced.
are
referenced.
If the matrix 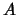 is not positive definite, the algorithm will
stop, trying to take the square root of a negative number in
equation 13.42.
is not positive definite, the algorithm will
stop, trying to take the square root of a negative number in
equation 13.42.
What about pivoting? Pivoting (i.e., the selection of a salubrious
pivot element for the division in Equation 13.43) is not
really required for the stability of the algorithm. In fact, the
only cause of failure is if the matrix 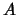 (or, with roundoff
error, another very nearby matrix) is not
positive definite.
(or, with roundoff
error, another very nearby matrix) is not
positive definite.




Next: QR factorization
Up: Annexes
Previous: Newton's method for non-linear
Contents
Frank Vanden Berghen
2004-04-19