


Next: Cholesky decomposition.
Up: Annexes
Previous: 1D Newton's search
Contents
Newton's method for non-linear equations
We want to find the solution 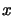 of the set of non-linear
equations:
of the set of non-linear
equations:
![$\displaystyle r(x)= \left[ \begin{array}{c} r_1(x) \\ \vdots \\
r_n(x) \end{array} \right] =0$](img1417.png) |
(13.31) |
The algorithm is the following:
- Choose
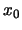
- Calculate a solution
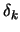 to the Newton equation:
to the Newton equation:
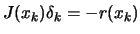 |
(13.32) |
-
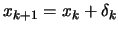
We use a linear model to derive the Newton step (rather than a
quadratical model as in unconstrained optimization) because the
linear model normally as a solution and yields an algorithm with
fast convergence properties (Newton's method has superlinear
convergence when the Jacobian 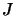 is a continuous function and
local quadratical convergence when
is a continuous function and
local quadratical convergence when 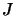 is Liptschitz continous).
Newton's method for unconstrained optimization can be derived by
applying Equation 13.32 to the set of nonlinear
equations
is Liptschitz continous).
Newton's method for unconstrained optimization can be derived by
applying Equation 13.32 to the set of nonlinear
equations
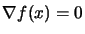 ).
).
Frank Vanden Berghen
2004-04-19
![$\displaystyle r(x)= \left[ \begin{array}{c} r_1(x) \\ \vdots \\
r_n(x) \end{array} \right] =0$](img1417.png)
![$\displaystyle r(x)= \left[ \begin{array}{c} r_1(x) \\ \vdots \\
r_n(x) \end{array} \right] =0$](img1417.png)