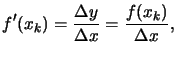


Next: Newton's method for non-linear
Up: Annexes
Previous: The secant equation
Contents
1D Newton's search
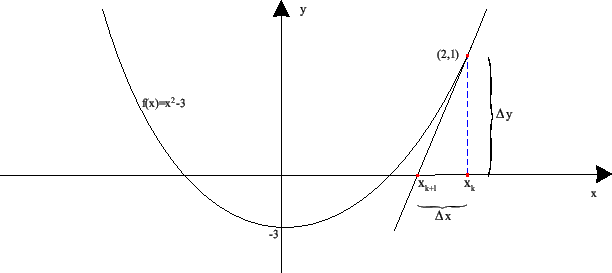
Suppose we want to find the root of
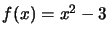 (see Figure
13.4). If our current estimate of the answer is
(see Figure
13.4). If our current estimate of the answer is
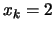 , we can get a better estimate
, we can get a better estimate 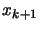 by drawing the
line that is tangent to
by drawing the
line that is tangent to 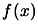 at
at
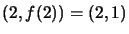 , and find the
point
, and find the
point 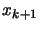 where this line crosses the x axis. Since,
and
we have that
where this line crosses the x axis. Since,
and
we have that
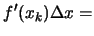 F
F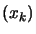
or
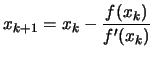 |
(13.30) |
which gives
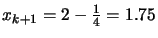 .
We apply the same process and iterate on
.
We apply the same process and iterate on 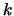 .
.
Figure 13.4:
A plot of
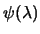 for
for 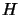 indefinite.
indefinite.
 |
Frank Vanden Berghen
2004-04-19