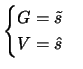


Next: Generating the final from
Up: The secondary Trust-Region subproblem
Previous: Generating .
Contents
Having generated 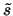 and
and 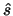 in the ways that have
been described, the algorithm sets
in the ways that have
been described, the algorithm sets 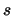 to a linear combination of
these vectors, but the choice is not restricted to
to a linear combination of
these vectors, but the choice is not restricted to
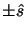 or
or
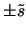 as suggested in the introduction of this
chapter(unless
as suggested in the introduction of this
chapter(unless 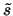 and
and 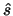 are nearly or exactly
parallel). Instead, the vectors
are nearly or exactly
parallel). Instead, the vectors 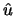 and
and 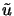 of unit
length are found in the span of
of unit
length are found in the span of 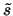 and
and 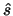 that
satisfy the condition
that
satisfy the condition
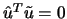 and
and
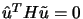 . The final
. The final 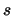 will be a combination of
will be a combination of 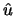 and
and 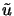 .
.
If we set:
We have
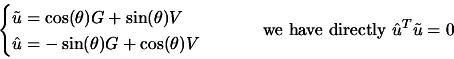 |
(5.8) |
We will now find 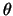 such
that
such
that
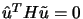 :
:
Using
We
obtain
Using the value of 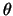 from Equation 5.10 in Equation
5.9 give the required
from Equation 5.10 in Equation
5.9 give the required 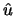 and
and 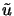 .
.



Next: Generating the final from
Up: The secondary Trust-Region subproblem
Previous: Generating .
Contents
Frank Vanden Berghen
2004-04-19