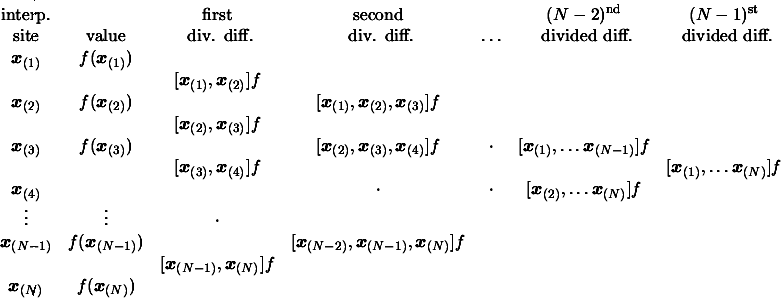Next: Multivariate Lagrange interpolation.
Up: Multivariate Lagrange Interpolation
Previous: Introduction
Contents
Subsections
We want to interpolate a simple curve
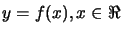 in the
plane (in
in the
plane (in 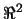 ). We have a set of
). We have a set of 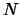 interpolation points
interpolation points
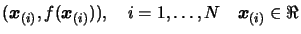 on the curve. We can choose N as we want. We must have
on the curve. We can choose N as we want. We must have
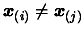 if
if 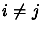 .
We define a Lagrange polynomial
.
We define a Lagrange polynomial 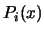 as
as
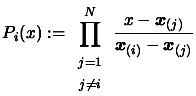 |
(3.2) |
We will have the following property:
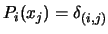 where
where
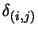 is the Kronecker delta:
is the Kronecker delta:
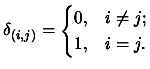 |
(3.3) |
Then, the interpolating polynomial 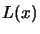 is:
is:
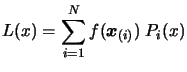 |
(3.4) |
This way to construct an interpolating polynomial is not very
effective because:
- The Lagrange polynomials
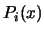 are all of degree
are all of degree 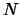 and
thus require lots of computing time for creation, evaluation and
addition (during the computation of
and
thus require lots of computing time for creation, evaluation and
addition (during the computation of 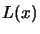 )...
)...
- We must know in advance all the
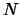 points. An iterative
procedure would be better.
points. An iterative
procedure would be better.
The solution to these problems : The Newton interpolation.
The Newton algorithm is iterative. We use the polynomial
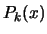 of degree
of degree 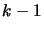 which already interpolates
which already interpolates 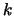 points
and transform it into a polynomial
points
and transform it into a polynomial 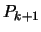 of degree
of degree 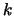 which
interpolates
which
interpolates 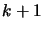 points of the function
points of the function 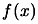 . We have:
. We have:
![$\displaystyle P_{k+1}(x)= P_k(x)+ \quad ( x- \boldsymbol{x}_{(1)}) \cdots (x-\boldsymbol{x}_{(k)})
\quad [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k+1)}]f$](img298.png) |
(3.5) |
The term
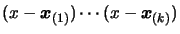 assures that the
second term of
assures that the
second term of 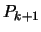 will vanish at all the points
will vanish at all the points
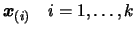 .
.
Definition:
![$ [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k+1)}]f$](img301.png) is called a
''divided difference''. It's the unique leading coefficient (that
is the coefficient of
is called a
''divided difference''. It's the unique leading coefficient (that
is the coefficient of 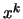 ) of the polynomial of degree
) of the polynomial of degree 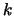 that
agree with
that
agree with 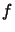 at the sequence
at the sequence
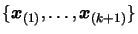 .
.
The final Newton interpolating polynomial is thus:
![$\displaystyle P(x)=
P_N(x) = \sum_{k=1}^N \quad ( x- \boldsymbol{x}_{(1)}) \cd...
...ymbol{x}_{(k-1)}
) \quad [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)}]f$](img304.png) |
(3.6) |
The final interpolation polynomial is the sum of polynomials of
degree varying from 0 to 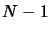 (see Equation 3.5). The
manipulation of the Newton polynomials (of Equation 3.5)
is faster than the Lagrange polynomials (of Equation 3.2)
and thus, is more efficient in term of computing time.
Unfortunately, with Newton polynomials, we don't have the nice
property that
(see Equation 3.5). The
manipulation of the Newton polynomials (of Equation 3.5)
is faster than the Lagrange polynomials (of Equation 3.2)
and thus, is more efficient in term of computing time.
Unfortunately, with Newton polynomials, we don't have the nice
property that
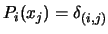 .
.
We can already write two basic properties of the divided
difference:
![$\displaystyle [ \boldsymbol{x}_{(k)} ]f= f( \boldsymbol{x}_{(k)})$](img306.png) |
(3.7) |
![$\displaystyle [ \boldsymbol{x}_{(1)}, \boldsymbol{x}_{(2)} ]f= \frac{f( \boldsy...
...(2)})- f(
\boldsymbol{x}_{(1)})}{\boldsymbol{x}_{(2)} - \boldsymbol{x}_{(1)} }$](img307.png) |
(3.8) |
Lemma 1
We will proof this by induction. First, we rewrite Equation
3.9, for N=1, using 3.7:
![$\displaystyle f(x)= f(\boldsymbol{x}_{(1)})
+ (x- \boldsymbol{x}_{(1)})[\boldsymbol{x}_{(1)}, x]f$](img309.png) |
(3.9) |
Using Equation 3.8 inside 3.10, we obtain:
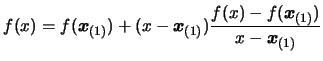 |
(3.10) |
This equation is readily verified. The case for 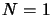 is solved.
Suppose the Equation 3.9 verified for
is solved.
Suppose the Equation 3.9 verified for 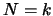 and proof
that it will also be true for
and proof
that it will also be true for 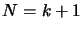 . First, let us rewrite
equation 3.10, replacing
. First, let us rewrite
equation 3.10, replacing
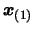 by
by
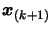 and
replacing
and
replacing 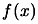 by
by
![$ [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)}, x]f $](img316.png) as
a function of x. (In other word, we will interpolate the function
as
a function of x. (In other word, we will interpolate the function
![$ f(x) \equiv [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)}, x]f $](img317.png) at the point
at the point
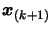 using 3.10.) We obtain:
using 3.10.) We obtain:
![$\displaystyle [\boldsymbol{x}_{(1)},
\ldots, \boldsymbol{x}_{(k)}, x]f = [\bol...
...,x] \bigg([\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)},
\cdot ]f \bigg)$](img318.png) |
(3.11) |
Let us rewrite Equation 3.9 with 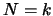 .
.
![$\displaystyle f(x)= P_k(x)
+ ( x- \boldsymbol{x}_{(1)}) \cdots (x-\boldsymbol{x}_{(k)} ) \quad [x_1, \ldots, x_k,
x]f$](img319.png) |
(3.12) |
Using Equation 3.12 inside Equation 3.13:
![$\displaystyle f(x)= P_{k+1}(x) + ( x- \boldsymbol{x}_{(1)}) \cdots (x-\boldsymb...
...,x] \bigg([\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)}, \cdot ]f
\bigg)$](img320.png) |
(3.13) |
Let us rewrite Equation 3.5 changing index 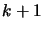 to
to
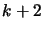 .
.
![$\displaystyle P_{k+2}(x)= P_{k+1}(x)+ \quad ( x- \boldsymbol{x}_{(1)}) \cdots
...
...ymbol{x}_{(k+1)}) \quad [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k+2)}]f$](img322.png) |
(3.14) |
Recalling the definition of the divided difference:
![$ [x_1, \ldots,
x_{k+2}]f$](img323.png) is the unique leading coefficient of the polynomial of
degree
is the unique leading coefficient of the polynomial of
degree 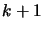 that agree with
that agree with 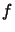 at the sequence
at the sequence
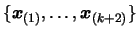 . Because of the uniqueness and comparing
equation 3.14 and 3.15, we see that (replacing
. Because of the uniqueness and comparing
equation 3.14 and 3.15, we see that (replacing 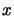 by
by
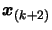 in 3.14):
in 3.14):
![$\displaystyle [\boldsymbol{x}_{(k+1)},\boldsymbol{x}_{(k+2)}]
\bigg([\boldsymb...
...k)}, \cdot ]f \bigg) = [\boldsymbol{x}_{(1)},
\ldots, \boldsymbol{x}_{(k+2)}]f$](img326.png) |
(3.15) |
Using Equation 3.16 inside 3.14:
![$\displaystyle f(x)=
P_{k+1}(x) + ( x- \boldsymbol{x}_{(1)}) \cdots (x-\boldsymbol{x}_{(k+1)} ) [\boldsymbol{x}_{(1)},
\ldots, \boldsymbol{x}_{(k+2)}]f$](img327.png) |
(3.16) |
Recalling the discussion of the paragraph after Equation
3.11, we can say then this last equation complete the
proof for 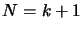 . The lemma 1 is now proved.
. The lemma 1 is now proved.
Lemma 2
This is clear from the definition of
![$ [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)}]f $](img329.png) .
.
Lemma 3
Combining Equation 3.16 and Equation 3.8, we
obtain:
![$\displaystyle \frac{ [\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k)}, \bold...
...\boldsymbol{x}_{(k+1)}}=[\boldsymbol{x}_{(1)}, \ldots, \boldsymbol{x}_{(k+2)}]f$](img331.png) |
(3.17) |
Using Equation 3.19 and lemma 2, we obtain directly
3.18. The lemma is proved.
Equation 3.18 has suggested the name ``divided difference''.
We can generate the entries of the divided difference table
column by column from the given dataset using Equation
3.18. The top diagonal then contains the desired
coefficients
![$ [\boldsymbol{x}_{(1)}]f $](img333.png) ,
,
![$ [\boldsymbol{x}_{(1)}, \boldsymbol{x}_{(2)}]f ,
[\boldsymbol{x}_{(1)}, \bolds...
...mbol{x}_{(3)}]f ,\ldots, [\boldsymbol{x}_{(1)}, \ldots,
\boldsymbol{x}_{(N)}]f$](img334.png) of the final Newton form of Equation 3.6.
Suppose we want to evaluate the following polynomial:
of the final Newton form of Equation 3.6.
Suppose we want to evaluate the following polynomial:
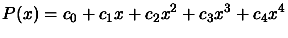 |
(3.18) |
We will certainly NOT use the following algorithm:
- Initialisation
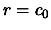
- For
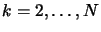
- Set
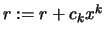
- Return
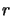
This algorithm is slow (lots of multiplications in 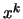 ) and
leads to poor precision in the result (due to rounding errors).
) and
leads to poor precision in the result (due to rounding errors).
The Horner scheme uses the following representation of the
polynomial 3.20:
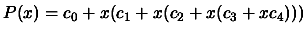 , to construct a very efficient evaluation algorithm:
, to construct a very efficient evaluation algorithm:
- Initialisation
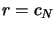
- For
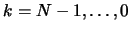
- Set
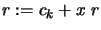
- Return
There is only 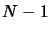 multiplication in this algorithm. It's thus
very fast and accurate.
multiplication in this algorithm. It's thus
very fast and accurate.




Next: Multivariate Lagrange interpolation.
Up: Multivariate Lagrange Interpolation
Previous: Introduction
Contents
Frank Vanden Berghen
2004-04-19
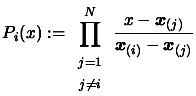
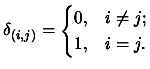
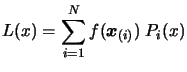
![\begin{figure}
\centering\fbox{\hspace{0.2cm}\parbox[t][1.6cm][b]{16cm}{
{\e...
...n which they occur in the argument list.}\\
}}\vspace{-0.1cm}
\end{figure}](img328.png)