



Next: Note about the validity
Up: The CONDOR unconstrained algorithm.
Previous: The CONDOR unconstrained algorithm.
Contents
The bound 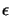 .
.
See Section 3.4.2 to know about 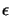 .
.
If we have updated the value of 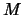 less than 10 times, we will
set
less than 10 times, we will
set
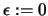 (see Section 3.4.1 to know about
(see Section 3.4.1 to know about
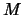 ). This is because we are not sure of the value of
). This is because we are not sure of the value of 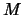 if it
has been updated less than 10 times.
if it
has been updated less than 10 times.
If the step size 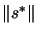 we have computed at step 3 of the
CONDOR algorithm is
we have computed at step 3 of the
CONDOR algorithm is
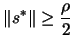 ,
then
,
then
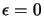 .
.
Otherwise,
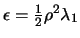 , where
, where
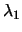 is an estimate of the slope of
is an estimate of the slope of 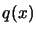 around
around
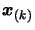 (see Section 4.10 to know how to compute
(see Section 4.10 to know how to compute
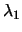 ).
).
We see that, when the slope is high, we permit a more
approximative (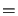 big value of
big value of 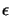 ) model of the function.
) model of the function.
Frank Vanden Berghen
2004-04-19