



Next: The parallel extension of
Up: The CONDOR unconstrained algorithm.
Previous: The bound .
Contents
Note about the validity check.
When the computation for the current 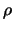 is complete, we check
the model (see step 14 of the algorithm) around
is complete, we check
the model (see step 14 of the algorithm) around
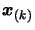 , then
one or both of the conditions:
, then
one or both of the conditions:
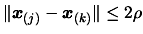 |
(6.5) |
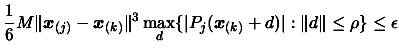 |
(6.6) |
must hold for every points in the
dataset. When 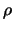 is reduced by formula 6.4, the
equation 6.5 is very often NOT verified. Only Equation
6.6, prevents the algorithm from sampling the model at
is reduced by formula 6.4, the
equation 6.5 is very often NOT verified. Only Equation
6.6, prevents the algorithm from sampling the model at
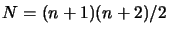 new points. Numerical experiments indicate that
the algorithm is highly successful in that it computes less then
new points. Numerical experiments indicate that
the algorithm is highly successful in that it computes less then
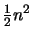 new points in most cases.
new points in most cases.
Frank Vanden Berghen
2004-04-19