


Next: Numerical Results of CONDOR.
Up: The CONDOR unconstrained algorithm.
Previous: Note about the validity
Contents
The parallel extension of CONDOR
We will use a client-server approach. The main node, the server
will have two concurrent process:
- The main process on the main computer is the classical
non-parallelized version of the algorithm, described at the
beginning of Chapter 6. There is an exchange of
information with the second/parallel process on steps 4 and 16 of
the original algorithm.
- The goal of the second/parallel process on the main
computer is to increase the quality of the model
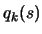 by using
client computers to sample
by using
client computers to sample 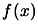 at specific interpolation sites.
at specific interpolation sites.
The client nodes are performing the following:
- Wait to receive from the second/parallel process on the
server a sampling site (a point).
- Evaluate the objective function at this site and return
immediately the result to the server.
- Go to step 1.
Several strategies have been tried to select good sampling sites.
We describe here the most promising one. The second/parallel task
is the following:
- A.
- Make a local copy
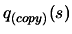 of
of 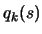 (and
of the associated Lagrange Polynomials
(and
of the associated Lagrange Polynomials 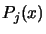 )
)
- B.
- Make a local copy
 of the dataset
of the dataset
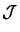
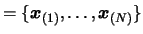 .
.
- C.
- Find the index
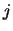 of the point inside
of the point inside
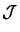
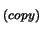 the further away from
the further away from
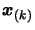 .
.
- D.
- Replace
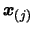 by a better point which will
increase the quality of the approximation of
by a better point which will
increase the quality of the approximation of 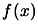 . The
computation of this point is done using Equation 3.38:
. The
computation of this point is done using Equation 3.38:
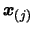 is replaced in
is replaced in
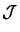
 by
by
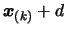 where
where
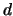 is the solution of the following problem:
is the solution of the following problem:
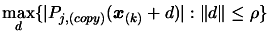 |
(6.7) |
- E.
- Ask for an evaluation the objective function at
point
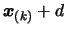 using a free client computer to performs the
evaluation. If there is still a client doing nothing, go back to
step C.
using a free client computer to performs the
evaluation. If there is still a client doing nothing, go back to
step C.
- F.
- Wait for a node to complete its evaluation of the
objective function
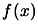 .
.
- G.
- Update
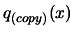 using this new evaluation.
Remove
using this new evaluation.
Remove 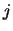 from
from
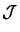
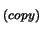 . go to step C.
. go to step C.
In the parallel/second process we are always working on a copy of
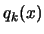 ,
,
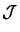 ,
,
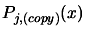 to avoid any side effect with
the main process which is guiding the search. The communication
and exchange of information between these two processes are done
only at steps 4 and 16 of the main algorithm described in the
previous section. Each time the main loop (main process) checks
the results of the parallel computations the following is done:
to avoid any side effect with
the main process which is guiding the search. The communication
and exchange of information between these two processes are done
only at steps 4 and 16 of the main algorithm described in the
previous section. Each time the main loop (main process) checks
the results of the parallel computations the following is done:
- i.
- Wait for the parallel/second task to enter the step
F described above and block the parallel task inside this step
F for the time needed to perform the points ii and
iii below.
- ii.
- Update of
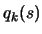 using all the points calculated in
parallel, discarding the points that are too far away from
using all the points calculated in
parallel, discarding the points that are too far away from 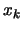 (at a distance greater than
(at a distance greater than 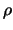 ). This update is performed
using technique described in Section 3.4.3 and Section
3.4.4. We will possibly have to update the index
). This update is performed
using technique described in Section 3.4.3 and Section
3.4.4. We will possibly have to update the index 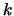 of the best point in the dataset
of the best point in the dataset
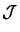 and
and 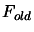 .
.
- iii.
- Perform operations described in point A &
B of the parallel/second task algorithm above: `` Copy
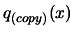 from
from 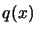 . Copy
. Copy
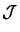
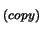 from
from
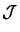
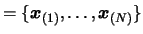 ``.
``.



Next: Numerical Results of CONDOR.
Up: The CONDOR unconstrained algorithm.
Previous: Note about the validity
Contents
Frank Vanden Berghen
2004-04-19