

Next: The secondary Trust-Region subproblem
Up: The Trust-Region subproblem
Previous: Termination Test.
Contents
An estimation of the slope of 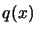 at the origin.
at the origin.
An estimation of the slope of 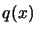 at the origin is given by
at the origin is given by
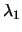 . In the optimization program, we will only compute
. In the optimization program, we will only compute
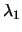 when we have interior convergence. The algorithm to
find
when we have interior convergence. The algorithm to
find 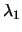 is the following:
is the following:
- Set
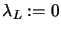 .
.
- Set
![$ \displaystyle \lambda_U := \min \bigg[ \max_i \Big[
[H]_{i,i} + \sum_{i\neq j } \vert [H]_{i,j} \vert \Big], \Vert H\Vert _F,
\Vert H\Vert _{\infty} \bigg] $](img728.png)
- Set
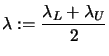
- Try to factorize
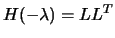 .
.
- Success: Set
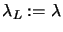
- Failure: Set
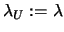
- If
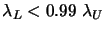 go back to step 3.
go back to step 3.
- The required value of
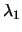 (=the approximation of the
slope at the origin) is inside
(=the approximation of the
slope at the origin) is inside 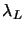
Frank Vanden Berghen
2004-04-19
![$ \displaystyle \lambda_U := \min \bigg[ \max_i \Big[
[H]_{i,i} + \sum_{i\neq j } \vert [H]_{i,j} \vert \Big], \Vert H\Vert _F,
\Vert H\Vert _{\infty} \bigg] $](img728.png)