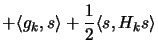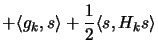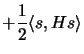


Next: must be positive definite.
Up: Unconstrained Optimization
Previous: The Lagrange Interpolation inside
Contents
The Trust-Region subproblem
We seek the solution 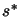 of the minimization problem:
of the minimization problem:
The following minimization problem is equivalent to the previous
one after a translation of the polynomial 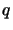 in the direction
in the direction
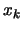 (see Section 3.4.6 about polynomial translation).
Thus, this problem will be discussed in this chapter:
(see Section 3.4.6 about polynomial translation).
Thus, this problem will be discussed in this chapter:
We will indifferently use the terms, polynomial, quadratic or
model. The ``trust region'' is defined by the set of all the
points which respects the constraint
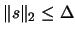 .
.
Definition: The trust region
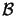
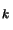 is the set of all points
such that
is the set of all points
such that

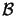
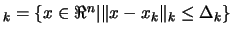 .
.
Note that we must always have at the end of the algorithm:
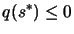 |
(4.1) |
The material of this chapter is based on the following references:
[CGT00c,MS83].
Subsections



Next: must be positive definite.
Up: Unconstrained Optimization
Previous: The Lagrange Interpolation inside
Contents
Frank Vanden Berghen
2004-04-19