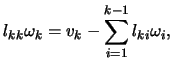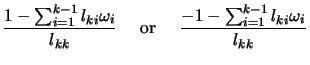Next: The Rayleigh quotient trick
Up: The Trust-Region subproblem
Previous: Initial values of and
Contents
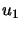 is the unit eigenvector corresponding to
is the unit eigenvector corresponding to 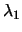 . We
need this vector in the hard case (see the paragraph containing
equation 4.15 ). Since
. We
need this vector in the hard case (see the paragraph containing
equation 4.15 ). Since 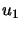 is the eigenvector
corresponding to
is the eigenvector
corresponding to 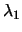 , we can write:
We will try to find a vector
, we can write:
We will try to find a vector 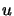 which minimizes
which minimizes
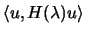 . This is equivalent to find a
vector
. This is equivalent to find a
vector 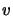 which maximize
which maximize
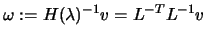 . We will choose the component of
. We will choose the component of 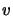 between
between 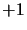 and
and
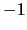 in order to make
in order to make 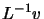 large. This is achieved by
ensuring that at each stage of the forward substitution
large. This is achieved by
ensuring that at each stage of the forward substitution
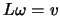 , the sign of
, the sign of 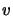 is chosen to make
is chosen to make 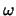 as large as
possible. In particular, suppose we have determined the first
as large as
possible. In particular, suppose we have determined the first
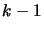 components of
components of 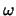 during the forward substitution, then
the
during the forward substitution, then
the
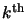 component satisfies:
and we pick
component satisfies:
and we pick 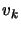 to be
to be 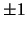 depending on which of
is larger. Having
found
depending on which of
is larger. Having
found 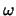 ,
, 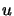 is simply
is simply
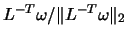 . The vector
. The vector 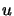 found this way has the useful property that
found this way has the useful property that
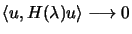
as
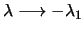




Next: The Rayleigh quotient trick
Up: The Trust-Region subproblem
Previous: Initial values of and
Contents
Frank Vanden Berghen
2004-04-19