Next:
An introduction to the
Up:
Thesis Constrained, non-linear, derivative-free
Previous:
Formal description
Contents
Unconstrained Optimization
Subsections
An introduction to the CONDOR algorithm.
Trust Region and Line-search Methods.
Conventions
General principle
Notion of Speed of convergence.
A simple line-search method: The Newton's method.
must be positive definite for Line-search methods.
Why is Newton's method crucial: Dennis-Moré theorem
Lemma 1.
Lemma 2.
Proof of Dennis-moré theorem.
A simple trust-region algorithm.
The basic trust-region algorithm (BTR).
About the CONDOR algorithm.
Multivariate Lagrange Interpolation
Introduction
A small reminder about univariate interpolation.
Lagrange interpolation
Newton interpolation
The divided difference for the Newton form.
The Horner scheme
Multivariate Lagrange interpolation.
The Lagrange polynomial basis
.
The Lagrange interpolation polynomial
.
The multivariate Horner scheme
The Lagrange Interpolation inside the optimization loop.
A bound on the interpolation error.
Validity of the interpolation in a radius of
around
.
Find a good point to replace in the interpolation.
Replace the interpolation point
by a new point
.
Generation of the first set of point
.
Translation of a polynomial.
The Trust-Region subproblem
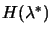must be positive definite.
Explanation of the Hard case.
Convex example.
Non-Convex example.
The hard case.
Finding the root of
.
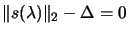Starting and safe-guarding Newton's method
How to pick
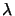inside
?
Initial values of
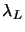and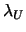
How to find a good approximation of
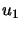: LINPACK METHOD
The Rayleigh quotient trick
Termination Test.
is near the boundary of the trust region: normal case
is inside the trust region: hard case
An estimation of the slope of
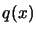at the origin.
The secondary Trust-Region subproblem
Generating
.
Generating
and
from
and
Generating the final
from
and
.
About the choice of
The CONDOR unconstrained algorithm.
The bound
.
Note about the validity check.
The parallel extension of CONDOR
Numerical Results of CONDOR.
Random objective functions
Hock and Schittkowski set
Parallel results on the Hock and Schittkowski set
Noisy optimization
Frank Vanden Berghen 2004-04-19
must be positive definite.
.
inside
![$ [\lambda _L \lambda _U]$](img14.png){kind=small}
?
and 
: LINPACK METHOD
at the origin.
must be positive definite for Line-search methods.
. 
.
around
.
by a new point 
.
.
is near the boundary
of the trust region: normal case
.
and 
from 
and 
from 
.