



Next: Constrained Optimization
Up: Numerical Results of CONDOR.
Previous: Parallel results on the
Contents
Noisy optimization
We will assume that objective functions derived from CFD codes have usually a
simple shape but are subject to high-frequency, low amplitude noise. This noise
prevents us to use simple finite-differences gradient-based algorithms. Finite-difference
is highly sensitive to the noise. Simple Finite-difference quasi-Newton algorithms
behave so badly because of the noise, that most researchers choose to use optimization
techniques based on GA,NN,... [CAVDB01,PVdB98,Pol00]. The poor performances of finite-differences
gradient-based algorithms are either due to the difficulty in choosing finite-difference
step sizes for such a rough function, or the often cited tendency of derivative-based
methods to converge to a local optimum [BDF$^+$98]. Gradient-based algorithms can still be
applied but a clever way to retrieve the derivative information must be used.
One such algorithm is DIRECT [GK95,Kel99,BK97] which is using a technique called implicit filtering.
This algorithm makes the same assumption about the noise (low amplitude, high
frequency) and has been successful in many cases [BK97,CGP$^+$01,SBT$^+$92]. For example, this optimizer has been used
to optimize the cost of fuel and/or electric power for the compressor stations
in a gas pipeline network [CGP$^+$01]. This is a two-design-variables optimization
problem. You can see in the right of Figure 7.5
a plot of the objective function. Notice the simple shape of the objective function
and the small amplitude, high frequency noise. Another family of optimizers is
based on interpolation techniques. DFO, UOBYQA and CONDOR belongs to this last
family. DFO has been used to optimize (minimize) a measure of the vibration of
a helicopter rotor blade [BDF$^+$98]. This problem is part of the Boeing problems
set [BCD$^+$95]. The blade are characterized by 31 design
variables. CONDOR will soon be used in industry on a daily basis to optimize the
shape of the blade of a centrifugal impeller [PMM$^+$03]. All these problems (gas pipeline, rotor
blade and impeller blade) have an objective function based on CFD code and are
both solved using gradient-based techniques. In particular, on the rotor blade
design, a comparative study between DFO and other approaches like GA, NN,... has
demonstrated the clear superiority of gradient-based techniques approach combined
with interpolation techniques [BDF$^+$98].
We will now illustrate the performances of CONDOR in two simple
cases which have sensibly the same characteristics as the
objective functions encountered in optimization based on CFD
codes. The functions, the amplitude of the artificial noise
applied to the objective functions (uniform noise distribution)
and all the parameters of the tests are summarized in Table
7.4. In this table ``NFE'' stands for Number of
Function Evaluations. Each columns represents 50 runs of the
optimizer.
Figure 7.3:
Noisy optimization.
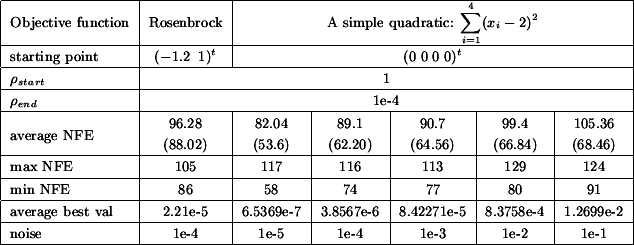 |
Figure 7.4:
On the left: A typical run for the
optimization of the noisy Rosenbrock function. On the right:Four
typical runs for the optimization of the simple noisy quadratic
(noise=1e-4).
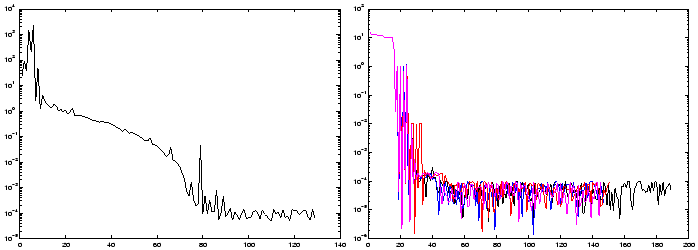 |
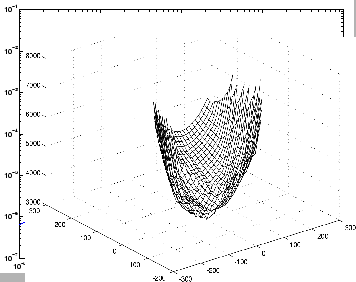
Figure 7.5:
On the left: The relation between the
noise (X axis) and the average best value found by the optimizer
(Y axis). On the right: Typical shape of objective function
derived from CFD analysis.
 |
A typical run for the optimization of the noisy Rosenbrock function is given in
the left of Figure 7.4. Four typical runs
for the optimization of the simple noisy quadratic in four dimension are given
in the right of figure 7.4. The noise
on these four runs has an amplitude of 1e-4. In these conditions, CONDOR stops
in average after 100 evaluations of the objective function but we can see in figure
7.4 that we usually already have found
a quasi-optimum solution after only 45 evaluations.
As expected, there is a clear relationship between the noise applied on the objective
function and the average best value found by the optimizer. This relationship
is illustrated in the left of figure 7.4.
From this figure and from the Table 7.4 we can
see the following: When you have a noise of 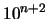 , the difference between the best value of the objective function
found by the optimizer AND the real value of the objective function at the optimum
is around
, the difference between the best value of the objective function
found by the optimizer AND the real value of the objective function at the optimum
is around 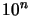 . In other words, in our case, if you apply a noise of
. In other words, in our case, if you apply a noise of 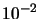 , you will get a final value of the objective function around
, you will get a final value of the objective function around
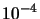 . Obviously, this strange result only holds for this simple
objective function (the simple quadratic) and these particular testing conditions.
Nevertheless, the robustness against noise is impressive.
. Obviously, this strange result only holds for this simple
objective function (the simple quadratic) and these particular testing conditions.
Nevertheless, the robustness against noise is impressive.
If this result can be generalized, it will have a great impact in
the field of CFD shape optimization. This simply means that if you
want a gain of magnitude 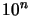 in the value of the objective
function, you have to compute your objective function with a
precision of at least
in the value of the objective
function, you have to compute your objective function with a
precision of at least 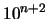 . This gives you an estimate of
the precision at which you have to calculate your objective
function. Usually, the more precision, the longer the evaluations
are running. We are always tempted to lower the precision to gain
in time. If this strange result can be generalized, we will be
able to adjust tightly the precision and we will thus gain a
precious time.
. This gives you an estimate of
the precision at which you have to calculate your objective
function. Usually, the more precision, the longer the evaluations
are running. We are always tempted to lower the precision to gain
in time. If this strange result can be generalized, we will be
able to adjust tightly the precision and we will thus gain a
precious time.




Next: Constrained Optimization
Up: Numerical Results of CONDOR.
Previous: Parallel results on the
Contents
Frank Vanden Berghen
2004-04-19


