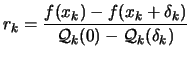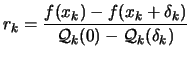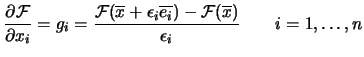Next: The basic trust-region algorithm
Up: An introduction to the
Previous: Trust Region and Line-search
Contents
A simple trust-region algorithm.
In all trust-region algorithms, we always choose
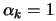 . The
length of the steps will be adjusted using
. The
length of the steps will be adjusted using 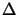 , the trust
region radius.
, the trust
region radius.
Recall that
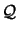
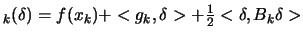 is the quadratical approximation
of
is the quadratical approximation
of
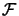
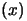 around
around 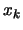 .
.
A simple trust-region algorithm is:
- solve
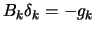 subject to
subject to
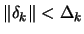 .
.
- Compute the ``degree of agreement''
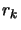 between
between
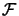 and
and
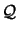 :
:
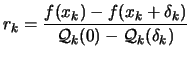 |
(2.15) |
- update
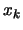 and
and 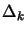 :
:
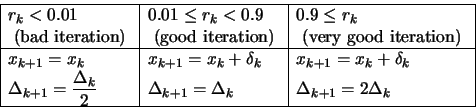 |
(2.16) |
- Increment
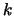 . Stop if
. Stop if
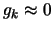 otherwise, go to step
1.
otherwise, go to step
1.
The main idea in this update is: only increase 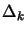 when
the local approximator
when
the local approximator
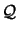 reflects well the real function
reflects well the real function
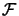 .
.
At each iteration of the algorithm, we need to have 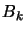 and
and
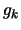 to compute
to compute 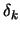 .
.
There are different ways for obtaining 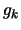 :
:
- Ask the user to provide a function which computes explicitly
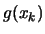 . The analytic form of the function to optimize should be
known in order to be able to derivate it.
. The analytic form of the function to optimize should be
known in order to be able to derivate it.
- Use an ``Automatic differentiation tool'' (like
``ODYSSEE''). These tools take, as input, the (fortran) code of
the objective function and generate, as output, the (fortran) code
which computes the function AND the derivatives of the function.
The generated code is called the ``adjoint code''. Usually this
approach
is very efficient in terms of CPU consumption.
If the time needed for one evaluation of 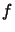 is 1 hour, than the
evaluation of
is 1 hour, than the
evaluation of 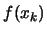 AND
AND 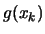 using the adjoint code will
take at most 3 hours (independently of the value of
using the adjoint code will
take at most 3 hours (independently of the value of 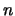 : the
dimension of the space). This result is very remarkable. One
drawback is the memory consumption of such methods which is very
high. For example, this limitation prevents to use such tools in
domain of ``Computational Fluid Dynamics'' code.
: the
dimension of the space). This result is very remarkable. One
drawback is the memory consumption of such methods which is very
high. For example, this limitation prevents to use such tools in
domain of ``Computational Fluid Dynamics'' code.
- Compute the derivatives of
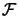
 using forward finite
differences:
using forward finite
differences:
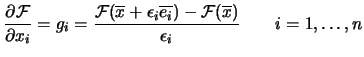 |
(2.17) |
If the
time needed for one evaluation of 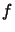 is 1 hour, then the
evaluation of
is 1 hour, then the
evaluation of 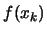 AND
AND 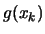 using this formulae will take
using this formulae will take
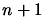 hours. This is indeed very bad. One advantage, is, if we
have
hours. This is indeed very bad. One advantage, is, if we
have 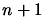 CPU's available, we can distribute the
computing load easily and obtain the results in 1 hour.
CPU's available, we can distribute the
computing load easily and obtain the results in 1 hour.
One major drawback is that
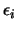 must be a very small
number in order to approximate correctly the gradient. If there is
a noise (even a small one) on the function evaluation, there is a
high risk that
must be a very small
number in order to approximate correctly the gradient. If there is
a noise (even a small one) on the function evaluation, there is a
high risk that 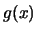 will be completely un-useful.
will be completely un-useful.
- Extract the derivatives from a (quadratic) polynomial which
interpolates the function at points close to
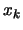 . This approach
has been chosen for CONDOR.
. This approach
has been chosen for CONDOR.
When there is noise on the objective function, we must choose the
interpolation sites very carefully. If we take points too close
from each other, we will get a poor model: it's destroyed by the
noise. If we take points very far from each other, we don't have
enough information about the local shape of the objective function
to guide correctly the search.
Beside, we need
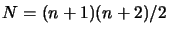 points to build a quadratic
polynomial. We cannot compute
points to build a quadratic
polynomial. We cannot compute 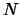 points at each iteration of the
algorithm. We will see in chapter 3 how to cope
with all these difficulties.
points at each iteration of the
algorithm. We will see in chapter 3 how to cope
with all these difficulties.
There are different ways for obtaining 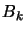 . Many are
unpractical. Here are some reasonable ones:
. Many are
unpractical. Here are some reasonable ones:
- Use a ``BFGS-update''. This update scheme uses the gradient
computed at each iteration to progressively construct the Hessian
matrix
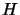 of
of 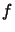 . Initially, we set
. Initially, we set 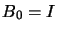 (the identity
matrix). If the objective function is quadratic, we will have
after
(the identity
matrix). If the objective function is quadratic, we will have
after 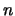 update,
update, 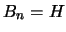 exactly (Since
exactly (Since 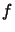 is a quadratic
polynomial,
is a quadratic
polynomial, 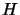 is constant over the whole space). If the
objective function is not a quadratical polynomial,
is constant over the whole space). If the
objective function is not a quadratical polynomial, 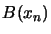 is
constructed using
is
constructed using
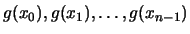 and is thus
a mixture of
and is thus
a mixture of
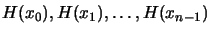 . This can lead
to poor approximation of
. This can lead
to poor approximation of 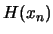 , especially if the curvature is
changing fast.
, especially if the curvature is
changing fast.
Another drawback is that 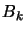 will always be positive definite.
This is very useful if we are using Line-search techniques but is
not appropriate in the case of trust-region method. In fact,
will always be positive definite.
This is very useful if we are using Line-search techniques but is
not appropriate in the case of trust-region method. In fact,
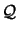
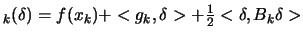 can be a very poor approximation of the real shape of the
objective function if, locally,
can be a very poor approximation of the real shape of the
objective function if, locally, 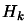 is indefinite or is negative
definite. This can lead to a poor search direction
is indefinite or is negative
definite. This can lead to a poor search direction 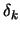 .
.
If there is noise on the objective function and if we are using a
finite difference approximation of the gradient, we will get a
poor estimate of the gradient of the objective function. Since
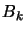 is constructed using only the gradients, it will also be a
very poor estimate of
is constructed using only the gradients, it will also be a
very poor estimate of 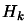 .
.
- Extract
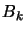 from a (quadratic) polynomial which
interpolates the function at points close to
from a (quadratic) polynomial which
interpolates the function at points close to 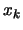 . This approach
has been chosen in CONDOR.
. This approach
has been chosen in CONDOR.
The point are chosen close to 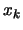 .
. 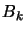 is thus never perturbed
by old, far evaluations.
is thus never perturbed
by old, far evaluations.
The points are ``far from each others'' to be less sensitive to
the
noise on the objective function.
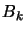 can also be positive, negative definite or indefinite. It
reflects exactly the actual shape of
can also be positive, negative definite or indefinite. It
reflects exactly the actual shape of 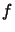 .
.




Next: The basic trust-region algorithm
Up: An introduction to the
Previous: Trust Region and Line-search
Contents
Frank Vanden Berghen
2004-04-19