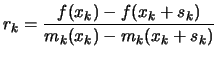


Next: About the CONDOR algorithm.
Up: An introduction to the
Previous: A simple trust-region algorithm.
Contents
Defnition: The trust region
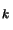 is the set of all points
such that
is the set of all points
such that
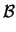 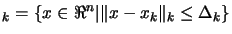 |
(2.18) |
The simple algorithm described in the Section 2.2 can be
generalized as follows:
- Initialization An initial point
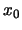 and an initial
trust region radius
and an initial
trust region radius 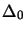 are given. The constants
are given. The constants  ,
,
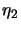 ,
, 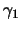 and
and 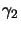 are also given and satisfy:
are also given and satisfy:
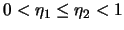 and and 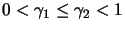 |
(2.19) |
Compute  and set
and set 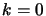
- Model definition Choose the norm
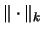 and
define a model
and
define a model 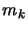 in
in
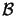
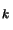
- Step computation Compute a step
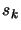 that
''sufficiently reduces the model''
that
''sufficiently reduces the model'' 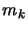 and such that
and such that
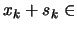
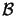
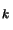
- Acceptance of the trial point. Compute
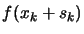 and define:
and define:
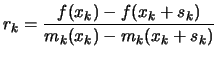 |
(2.20) |
If
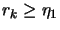 , then define
, then define
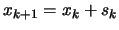 ; otherwise define
; otherwise define
 .
.
- Trust region radius update. Set
 |
(2.21) |
Increment 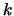 by 1 and go to step
2.
by 1 and go to step
2.
Under some very weak assumptions, it can be proven that this
algorithm is globally convergent to a local optimum [CGT00a].
The proof will be skipped.



Next: About the CONDOR algorithm.
Up: An introduction to the
Previous: A simple trust-region algorithm.
Contents
Frank Vanden Berghen
2004-04-19