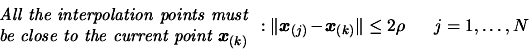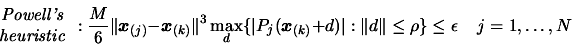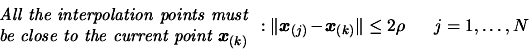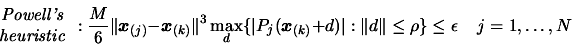Next: Parallel results on the
Up: Numerical Results of CONDOR.
Previous: Random objective functions
Contents
Hock and Schittkowski set
The tests problems are arbitrary and have been chosen by A.R.Conn, K. Scheinberg
and Ph.L. Toint. to test their DFO algorithm. The performances of DFO are thus
expected to be, at least, good. We list the number of function evaluations that
each algorithm took to solve the problem. We also list the final function values
that each algorithm achieved. We do not list the CPU time, since it is not relevant
in our context. The ``*'' indicates that an algorithm terminated early because
the limit on the number of iterations was reached. The default values for all
the parameters of each algorithm is used. The stopping tolerance of DFO was set
to 1e-4, for the other algorithms the tolerance was set to appropriate comparable
default values. The comparison between the algorithms is based on the number of
function evaluations needed to reach the SAME precision. For the most fair comparison
with DFO, the stopping criteria (
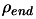 ) of CONDOR has been chosen so that CONDOR is always stopping
with a little more precision on the result than DFO. This precision is sometime
insufficient to reach the true optima of the objective function. In particular,
in the case of the problems GROWTHLS and HEART6LS, the CONDOR algorithm can find
a better optimum after some more evaluations (for a smaller
) of CONDOR has been chosen so that CONDOR is always stopping
with a little more precision on the result than DFO. This precision is sometime
insufficient to reach the true optima of the objective function. In particular,
in the case of the problems GROWTHLS and HEART6LS, the CONDOR algorithm can find
a better optimum after some more evaluations (for a smaller
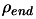 ). All algorithms were implemented in Fortran 77 in double
precision except COBYLA which is implemented in Fortran 77 in single precision
and CONDOR which is written in C++ (in double precision). The trust region minimization
subproblem of the DFO algorithm is solved by NPSOL [GMSM86], a fortran 77 non-linear optimization package
that uses an SQP approach. For CONDOR, the number in parenthesis indicates the
number of function evaluation needed to reach the optimum without being assured
that the value found is the real optimum of the function. For example, for the
WATSON problem, we find the optimum after (580) evaluations. CONDOR still continues
to sample the objective function, searching for a better point. It's loosing 87
evaluations in this search. The total number of evaluation (reported in the first
column) is thus 580+87=667.
). All algorithms were implemented in Fortran 77 in double
precision except COBYLA which is implemented in Fortran 77 in single precision
and CONDOR which is written in C++ (in double precision). The trust region minimization
subproblem of the DFO algorithm is solved by NPSOL [GMSM86], a fortran 77 non-linear optimization package
that uses an SQP approach. For CONDOR, the number in parenthesis indicates the
number of function evaluation needed to reach the optimum without being assured
that the value found is the real optimum of the function. For example, for the
WATSON problem, we find the optimum after (580) evaluations. CONDOR still continues
to sample the objective function, searching for a better point. It's loosing 87
evaluations in this search. The total number of evaluation (reported in the first
column) is thus 580+87=667.
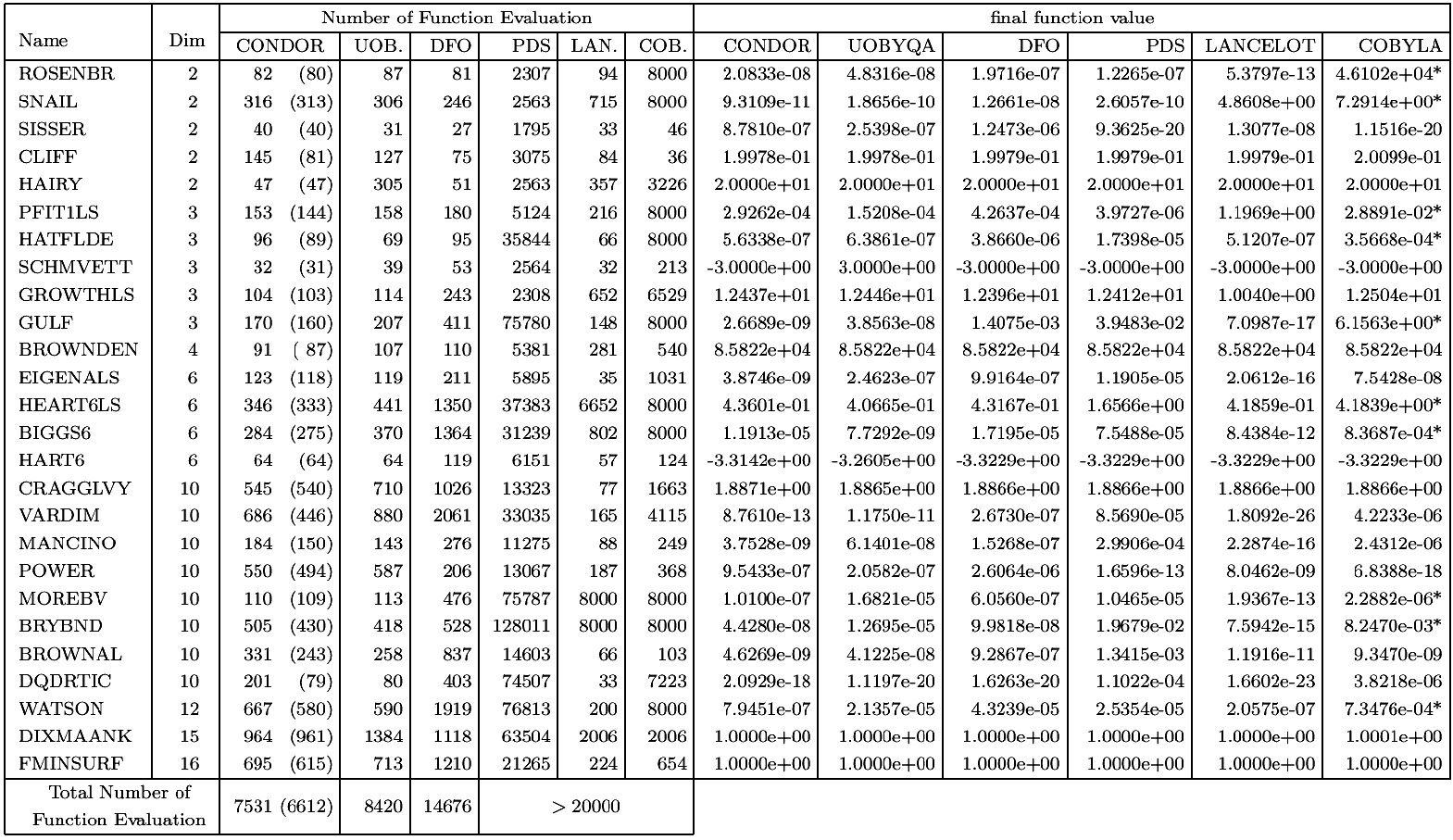
CONDOR and UOBYQA are both based on the same ideas and have nearly the same behavior.
Small differences can be due to the small difference between algorithms of Chapter
4&5
and the algorithms used inside UOBYQA.
PDS stands for ``Parallel Direct Search'' [DT91]. The number of function evaluations is high
and so the method doesn't seem to be very attractive. On the other hand, these
evaluations can be performed on several CPU's reducing considerably the computation
time.
Lancelot [CGT92] is a code for large scale optimization when
the number of variable is 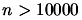 and the objective function is easy to evaluate (less than
and the objective function is easy to evaluate (less than
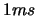 .). Its model is build using finite differences and BFGS update.
This algorithm has not been design for the kind of application we are interested
in and is thus performing accordingly.
.). Its model is build using finite differences and BFGS update.
This algorithm has not been design for the kind of application we are interested
in and is thus performing accordingly.
COBYLA [Pow94] stands for ``Constrained Optimization by
Linear Approximation'' by Powell. It is, once again, a code designed for
large scale optimization. It is a derivative free method, which uses linear polynomial
interpolation of the objective function.
DFO [CST97,CGT98] is an algorithm by A.R.Conn, K. Scheinberg
and Ph.L. Toint. It's very similar to UOBYQA and CONDOR. It has been specially
designed for small dimensional problems and high-computing-load objective functions.
In other words, it has been designed for the same kind of problems that CONDOR.
DFO also uses a model build by interpolation. It is using a Newton polynomial
instead of a Lagrange polynomial. When the DFO algorithm starts, it builds a linear
model (using only 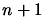 evaluations of the objective function;
evaluations of the objective function; 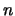 is the dimension of the search space) and then directly uses this
simple model to guide the research into the space. In DFO, when a point is ``too
far'' from the current position, the model could be invalid and could
not represent correctly the local shape of the objective function. This ``far
point'' is rejected and replaced by a closer point. This operation unfortunately
requires an evaluation of the objective function. Thus, in some situation, it
is preferable to lower the degree of the polynomial which is used as local model
(and drop the ``far'' point), to avoid this evaluation. Therefore, DFO is using
a polynomial of degree oscillating between 1 and a ''full'' 2. In UOBYQA and CONDOR,
we use the Moré and Sorenson algorithm [MS83,CGT00c] for the computation of the trust region step.
It is very stable numerically and give very high precision results. On
the other hand, DFO uses a general purpose tool (NPSOL [GMSM86]) which gives high quality results but
that cannot be compared to the Moré and Sorenson algorithm when precision
is critical. An other critical difference between DFO and CONDOR/UOBYQA is the
formula used to update the local model. In DFO, the quadratical model built at
each iteration is not defined uniquely. For a unique quadratical model in
is the dimension of the search space) and then directly uses this
simple model to guide the research into the space. In DFO, when a point is ``too
far'' from the current position, the model could be invalid and could
not represent correctly the local shape of the objective function. This ``far
point'' is rejected and replaced by a closer point. This operation unfortunately
requires an evaluation of the objective function. Thus, in some situation, it
is preferable to lower the degree of the polynomial which is used as local model
(and drop the ``far'' point), to avoid this evaluation. Therefore, DFO is using
a polynomial of degree oscillating between 1 and a ''full'' 2. In UOBYQA and CONDOR,
we use the Moré and Sorenson algorithm [MS83,CGT00c] for the computation of the trust region step.
It is very stable numerically and give very high precision results. On
the other hand, DFO uses a general purpose tool (NPSOL [GMSM86]) which gives high quality results but
that cannot be compared to the Moré and Sorenson algorithm when precision
is critical. An other critical difference between DFO and CONDOR/UOBYQA is the
formula used to update the local model. In DFO, the quadratical model built at
each iteration is not defined uniquely. For a unique quadratical model in 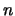 variables one needs at least
variables one needs at least
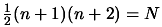 points and their function values. ``In DFO,
models are often build using many fewer points and such models are not uniquely
defined'' (citation from [CGT98]). The strategy used inside DFO is to select
the model with the smallest Frobenius norm of the Hessian matrix. This update
is highly numerically instable [Pow04]. Some recent research at this subject have
maybe found a solution [Pow04] but this is still ``work in progress''. The
model DFO is using can thus be very inaccurate.
points and their function values. ``In DFO,
models are often build using many fewer points and such models are not uniquely
defined'' (citation from [CGT98]). The strategy used inside DFO is to select
the model with the smallest Frobenius norm of the Hessian matrix. This update
is highly numerically instable [Pow04]. Some recent research at this subject have
maybe found a solution [Pow04] but this is still ``work in progress''. The
model DFO is using can thus be very inaccurate.
In CONDOR and in UOBYQA the validity of the model is checked
using the two Equations 6.5 and 6.6, which are
restated here for clarity:
The first equation (6.5) is also used in DFO.
The second equation (6.6) is NOT used in DFO.
This last equation allows us to ''keep far points'' inside the model, still being
assured that it is valid. It allows us to have a ``full'' polynomial of second
degree for a ``cheap price''. The DFO algorithm cannot use equation 6.6
to check the validity of its model because the variable 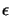 (which is computed in UOBYQA and in CONDOR as a by-product
of the computation of the ``Moré and Sorenson Trust Region Step'') is not
cheaply available. In DFO, the trust region step is calculated using an external
tool: NPSOL [GMSM86].
(which is computed in UOBYQA and in CONDOR as a by-product
of the computation of the ``Moré and Sorenson Trust Region Step'') is not
cheaply available. In DFO, the trust region step is calculated using an external
tool: NPSOL [GMSM86]. 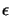 is difficult to obtain and is not used.
is difficult to obtain and is not used.
UOBYQA and CONDOR are always using a full quadratical model. This enables us to
compute Newton's steps. The Newton's steps have a proven quadratical convergence
speed [DS96]. Unfortunately, some evaluations of the objective
function are lost to build the quadratical model. So, we only obtain *near* quadratic
speed of convergence. We have Q-superlinear convergence (see original paper of
Powell [Pow00]). (In fact the convergence speed is often directly
proportional to the quality of the approximation 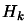 of the real Hessian matrix of
of the real Hessian matrix of 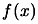 ). Usually, the price (in terms of number of function evaluations)
to construct a good quadratical model is very high but using equation (6.6),
UOBYQA and CONDOR are able to use very few function evaluations to update the
local quadratical model.
). Usually, the price (in terms of number of function evaluations)
to construct a good quadratical model is very high but using equation (6.6),
UOBYQA and CONDOR are able to use very few function evaluations to update the
local quadratical model.
When the dimension of the search space is greater than 25, the time needed to
start, building the first quadratic, is so important (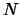 evaluations) that DFO may becomes attractive again. Especially, if
you don't want the optimum of the function but only a small improvement in a small
time. If several CPU's are available, then CONDOR once again imposes itself. The
function evaluations needed to build the first quadratic are parallelized on all
the CPU's without any loss of efficiency when the number of CPU increases (the
maximum number of CPU is
evaluations) that DFO may becomes attractive again. Especially, if
you don't want the optimum of the function but only a small improvement in a small
time. If several CPU's are available, then CONDOR once again imposes itself. The
function evaluations needed to build the first quadratic are parallelized on all
the CPU's without any loss of efficiency when the number of CPU increases (the
maximum number of CPU is 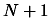 ). This first construction phase has a great parallel efficiency,
as opposed to the rest of the optimization algorithm where the efficiency becomes
soon very low (with the number of CPU increasing). In contrast to CONDOR, the
DFO algorithm has a very short initialization phase and a long research phase.
This last phase can't be parallelized very well. Thus, when the number of CPU's
is high, the most promising algorithm for parallelization is CONDOR. A parallel
version of CONDOR has been implemented. Very encouraging experimental results
on the parallel code are given in the next section.
). This first construction phase has a great parallel efficiency,
as opposed to the rest of the optimization algorithm where the efficiency becomes
soon very low (with the number of CPU increasing). In contrast to CONDOR, the
DFO algorithm has a very short initialization phase and a long research phase.
This last phase can't be parallelized very well. Thus, when the number of CPU's
is high, the most promising algorithm for parallelization is CONDOR. A parallel
version of CONDOR has been implemented. Very encouraging experimental results
on the parallel code are given in the next section.
When the local model is not convex, no second order convergence proof (see [CGT00d]) is available. It means that, when using
a linear model, the optimization process can prematurely stop. This phenomenon
*can* occur with DFO which uses from time to time a simple linear model. CONDOR
is very robust and always converges to a local optimum (extensive numerical tests
have been made [VB04]).
From the numerical results, the CONDOR algorithm (on 1 CPU) outperforms the DFO
algorithm when the dimension of the search space is greater than two. This result
can be explained by the fact that, most of the time, DFO uses a simple linear
approximation (with few or no second degree terms) of the objective function to
guide its search. This poor model gives ``sufficiently'' good search directions
when 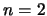 . But when
. But when 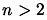 , the probability to choose a bad search direction is higher.
The high instability of the least-Frobenius-norm update of the model used in DFO
can also give poor model, degrading the speed of the algorithm.
, the probability to choose a bad search direction is higher.
The high instability of the least-Frobenius-norm update of the model used in DFO
can also give poor model, degrading the speed of the algorithm.




Next: Parallel results on the
Up: Numerical Results of CONDOR.
Previous: Random objective functions
Contents
Frank Vanden Berghen
2004-04-19