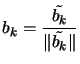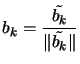


Next: Notions of constrained optimization
Up: Annexes
Previous: Line-Search addenda.
Contents
Subsections
We have a set of independent vectors
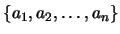 . We want to convert it into a set of orthonormal vectors
. We want to convert it into a set of orthonormal vectors
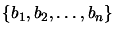 by the Gram-Schmidt process.
by the Gram-Schmidt process.
The scalar product between vectors 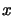 and
and 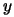 will be noted
will be noted 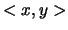
- Initialization
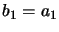 ,
, 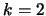
- Orthogonalisation
 |
(13.15) |
We will take 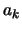 and transform
it into
and transform
it into
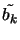 by removing from
by removing from 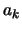 the component of
the component of
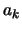 parallel to all the previously determined
parallel to all the previously determined 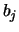 .
.
- Normalisation
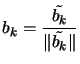 |
(13.16) |
- Loop increment
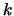 . If
. If 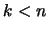 go to step 2.
go to step 2.
Algorithm 2.
- Initialization k=1;
- Normalisation
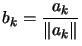 |
(13.17) |
- Orthogonalisation for
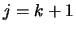 to
to 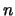 do:
do:
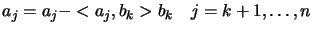 |
(13.18) |
We will take the 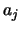 which are left and remove from all of them the component parallel
to the current vector
which are left and remove from all of them the component parallel
to the current vector 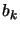 .
.
- Loop increment
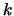 . If
. If 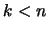 go to step 2.
go to step 2.



Next: Notions of constrained optimization
Up: Annexes
Previous: Line-Search addenda.
Contents
Frank Vanden Berghen
2004-04-19