Numerical Results for the constrained algorithm

We will compare CONDOR with other optimizers on constrained test problems from the set of Hock and Schittkowski [HS81]. All the constraints of the problems from the Hock and Schittkowski set were qualified as ``easy'' constraints. We list the number of function evaluations that each algorithm took to solve the problem. We also list the final function values that each algorithm achieved. We do not list the CPU time, since it is not relevant in our context. The ``*'' symbol next to the function values in the DFO column indicates that the algorithm terminated early because the trust region minimization algorithm failed to produce a feasible solution. Even when the DFO algorithm terminates early, it often does so after finding a local optimal solution, as in the case of HS54 and HS106. In other columns, the ``*'' indicates that an algorithm terminated early because the limit on the number of iterations was reached.

The descriptions in AMPL (''Advanced Mathematical Programming Language'') (see [FGK02] about AMPL) of the optimization problems are given in the code section 14.2. All the starting points are the default ones used in the literature and are found in the AMPL file.

The stopping tolerances of CONDOR and DFO were set to 1e-4, for the other algorithms the tolerance was set to appropriate comparable default values. In the constrained case, the stopping criteria algorithm for CONDOR is not very performant. Indeed, very often, the optimal value of the function is found since a long time and the optimizer is still running. The number in parenthesis for the CONDOR algorithm gives the number of function evaluations needed to reach the optimum (or, at least, the final value given in the table). Unfortunately, some extra, un-useful evaluations are performed. The total is given in the column 1 of the CONDOR results. In particular, for problem hs268, the optimum is found after only 25 function evaluations but CONDOR still performs 152 more useless evaluations (leading to the total of 177 evaluations reported in the table).

All algorithms were implemented in Fortran 77 in double precision except COBYLA which is implemented in Fortran 77 in single precision and CONDOR which is written in C++ (in double precision). The trust region minimization subproblem of the DFO algorithm is solved by NPSOL [GMSM86], a fortran 77 non-linear optimization package that uses an SQP approach.

 

		Number of Function Evaluation					final function value
Name	Dim	CONDOR		DFO	LAN.	COB.	CONDOR	DFO	LAN.	COB.
hs022	2	13	(1)	15	24	24	1.0000e+00	1.0000e+00	1.0000e+00	1.0000e+00
hs023	2	11	(9)	16	1456	28	2.0000e+00	2.0000e+00	2.0000e+00	2.0000e+00
hs026	3	115	(49)	49	1677	1001	2.7532e-13	1.9355e-09	6.1688e-09	1.0250e-07
hs034	3	21	(18)	22	405	41	-8.3403e-01	-8.3403e-01	-8.3403e-01	-8.3403e-01
hs038	4	311	(245)	536	128	382	7.8251e-13	1.6583e-07	4.3607e-13	7.8770e+00
hs044	4	23	(18)	26	35	45	-1.5000e+01	-1.5000e+01	-1.5000e+01	-1.5000e+01
hs065	3	20	(17)	35	1984	102	9.5352e-01	9.5352e-01	9.5352e-01	9.5352e-01
hs076	4	21	(17)	29	130	76	-4.6818e+00	-4.6818e+00	-4.6818e+00	-4.6818e+00
hs100	7	48	(38)	127	6979	175	6.8199e+02	6.8063e+02	6.9138e+02*	6.8063e+02
hs106	8	201	(103)	63	196	93	8.9882e+03	7.0492e+03*	1.4995e+04	1.4994e+04
hs108	9	90	(77)	62	2416	177	-7.8167e-01	-8.6603e-01	-8.6602e-01	-8.6603e-01
hs116	13	141	(118)	87	12168	119	8.0852e+01	9.7485e+01*	5.0000e+01	3.5911e+02
hs268	5	177	(25)	84	5286	676	-1.5917e-11	-1.8190e-11	2.6576e+01	5.9238e+00

From the experimental results, we can see that the CONDOR algorithm performs very well compared to the other algorithms on problems with linear constraints only. On these problems (hs038, hs044, hs076, hs268), the step is always calculated using a reduced-space version of the Moré and Sorensen algorithm of Chapter 4 and is thus very accurate. When using the Moré and Sorensen algorithm, the variable 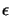$\epsilon$ needed to use the bound of Equation 6.6 is computed. We have seen in Section 7.2 that:

• Equation 6.6 is not used by DFO.
• Equation 6.6 allows very fast convergence speed.

These facts explain the superior performance of CONDOR on box and linear constraints.

The starting point of problem hs022 is infeasible. When this situation occurs, CONDOR searches for the closest feasible point from the given starting point. Once this ``feasibility restoration phase'' is finished, the real optimization process begins: the optimizer asks for evaluations of the objective function. In problem hs022 the point which is found after the ``feasibility restoration phase'' is also the optimum of the objective function. This explains the value ``1'' in parenthesis for this problem for the CONDOR algorithm.

For the problem hs116, the value of the objective function at the optimum is 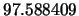$97.588409$. The problem is so badly scaled that LANCELOT and CONDOR are both finding an infeasible point as result. Among all the problems considered, this difficulty arises only for problem hs116. During the development of the optimizer, I had to laugh a little because, on this problem, on some iterations, the Hessian matrix is filled with number of magnitude around 1e40 and the gradient vector is filled with number of magnitude around 1e-10. That's no surprise that the algorithm that compute the step is a little ``lost'' in these conditions!

The problems where chosen by A.R.Conn, K.Schneinberg and Ph.L.Toint to test their DFO algorithm, during its development. Thus, the performance of DFO on these problems is expected to be very good or, at least, good. The problems hs034, hs106 and hs116 have linear objective functions. The problems hs022, hs023, hs038, hs044, hs065, hs076, hs100 and hs268 have quadratical objective functions. The problems hs026, hs065 and hs100 have few simple non-linear terms in the objective function. The problems are not chosen so that CONDOR outperforms the other algorithms. The test set is arbitrary and not tuned for CONDOR. However, this test-set has been used during CONDOR's development for debug purposes. In fact, this test-set is particularly well-suited for DFO because the objective function is very ``gentle'', mostly linear with very few quadratic/non-linear terms. In these conditions, using a near-linear model for the objective function is a good idea. That's exactly what DFO does (and not CONDOR). The main difficulty here is really the constraints.

On the problem hs268 which has only simple linear constraints, Lancelot and COBYLA are both failing. The constraints on these problems are qualified as ``gentle'' but is it really the case? CONDOR was tested on many other more gentle, constrained objective functions during its development and everything worked fine.

The less good results are obtained for problems with badly scaled non-linear constraints (hs108, h116). On these problems, the quality of the QP algorithm is very important. The home-made QP shows unfortunately its limits. A good idea for future extension of CONDOR is to implement a better QP.

These results are very encouraging. Despite its simple implementation, CONDOR is competitive compared to high-end, commercial optimizers. In the field of interest, where we encounter mostly box or linear constraints, CONDOR seems to have the best performances (at least, on this reduced test set).