



Next: Some advice on how
Up: Conclusions
Previous: About the code
Contents
Subsections
The algorithm is still limited to search space of dimension lower
than 50 (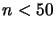 ). This limitation has two origin:
). This limitation has two origin:
- The number of evaluation of the function needed to construct
the first interpolation polynomial is very high:
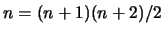 ). It is possible to build a quadratic using less
point (using a ``Least frobenius norm updating of quadratic models
that satisfy interpolation conditions''), as in the DFO algorithm,
but the technique seems currently numerically very instable. Some
recent works of Powell about this subject suggest
that maybe a solution will soon be found (see [Pow02]).
). It is possible to build a quadratic using less
point (using a ``Least frobenius norm updating of quadratic models
that satisfy interpolation conditions''), as in the DFO algorithm,
but the technique seems currently numerically very instable. Some
recent works of Powell about this subject suggest
that maybe a solution will soon be found (see [Pow02]).
- The algorithm to update the Lagrange polynomial (when we
replace one interpolation point by another) is very slow. Its
complexity is
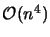 . Since the calculation involved are
very simple, it should be possible to parallelize this process.
Another solution would be to use ``Multivariate Newton
polynomials'' instead of ``Multivariate Lagrange Polynomials''.
. Since the calculation involved are
very simple, it should be possible to parallelize this process.
Another solution would be to use ``Multivariate Newton
polynomials'' instead of ``Multivariate Lagrange Polynomials''.
Other improvements are possible:
- Improve the ``warm-start'' capabilities of the algorithm.
- Use a better strategy for the parallel case (see end of
section 7.3)
- Currently the trust region is a simple ball: this is linked
to the L2-norm
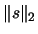 used in the trust region step
computation of Chapter 4. It would be interesting to
have a trust region which reflects the underlying geometry of the
model and not give undeserved weight to certain directions (like
by using a H-norm: see Section 12.4 about this norm).
The Dennis-Moré algorithm can be easily modified to use the
H-norm. This improvement will have a small effect
provided the variables have already been correctly normalized (see
section 12.3 about normalization).
used in the trust region step
computation of Chapter 4. It would be interesting to
have a trust region which reflects the underlying geometry of the
model and not give undeserved weight to certain directions (like
by using a H-norm: see Section 12.4 about this norm).
The Dennis-Moré algorithm can be easily modified to use the
H-norm. This improvement will have a small effect
provided the variables have already been correctly normalized (see
section 12.3 about normalization).
- The Dennis-Moré algorithm of of Chapter 4
requires many successive Cholesky factorization of the matrix
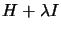 , with different value of
, with different value of 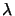 . It's possible to
partially transform
. It's possible to
partially transform 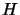 in tri-diagonal form to speed-up the
successive Cholesky factorizations, as explained in [Pow97].
in tri-diagonal form to speed-up the
successive Cholesky factorizations, as explained in [Pow97].
- Another possible improvement would be to use a more clever
algorithm for the update of the two trust regions radius
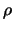 and
and 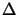 . In particular, the update of
. In particular, the update of 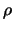 is actually not
linked at all to the success of the polynomial interpolation. It
can be improved.
is actually not
linked at all to the success of the polynomial interpolation. It
can be improved.
- Some researches can also be made in the field of kriging
models (see [BDF$^+$98]). These models need very few ``model
improvement steps'' to obtain a good validity. The
validity of the approximation can also be easily checked. On the
contrary, in optimization algorithms based on other models (or
surrogate: see [KLT97,BDF$^+$99]) like Neural Networks, Fuzzy Set,
Lazy learning, ... the validity of the model is hard to
assess (there is often no mathematical tool to allow this). The
surrogate approach is a serious, correct and strong theory.
Unfortunately, most optimizers based on NN, Fuzzy set,... do not
implement completely the surrogate approach. In particular, most
of the time, these kind of optimizers doesn't care for the
validity of their model. They should thus be proscribed because
they can easily fail to converge, even to a simple local optimum.
Furthermore, they usually need many ``model improvement step'' to
ensure validity and turn to be very slow.
Constrained case
The home-made QP is not very performant and could be upgraded.
Currently, we are using an SQP approach to handle non-linear
constraints. It could be interesting to use a penalty-function
approach.
When the model is invalid, we have to sample the objective
function at a point of the space which will increase substantially
the quality of the model. This point is calculated using Equation
3.38:
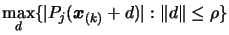 |
(12.1) |
The method to solve this equation is
described in Chapter 5. This method does not take
into account the constraints. As a result, CONDOR may ask for some
evaluations of the objective function in the infeasible space. The
infeasibility is never excessive (it's limited by 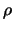 : see
equation 12.1 ) but can sometime be a problem. A major
improvement is to include some appropriate techniques to have a
fully feasible-only algorithm.
: see
equation 12.1 ) but can sometime be a problem. A major
improvement is to include some appropriate techniques to have a
fully feasible-only algorithm.
Sometimes the evaluation of the objective function fails. This
phenomenon is usual in the field of shape design optimization by
CFD code. It simply means that the CFD code has not converged.
This is referred in the literature as ``virtual constraints''
[CGT98]. In this case, a simple strategy is to reduce the Trust
Region radius 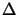 and continue normally the optimization
process. This strategy has been implemented and tested on some
small examples and shows good results. However, It is still in
development and tuning phase. It is the subject of current,
ongoing research.
and continue normally the optimization
process. This strategy has been implemented and tested on some
small examples and shows good results. However, It is still in
development and tuning phase. It is the subject of current,
ongoing research.




Next: Some advice on how
Up: Conclusions
Previous: About the code
Contents
Frank Vanden Berghen
2004-04-19