



Next: Preliminary research
Up: The METHOD project
Previous: The METHOD project
Contents
A shape can be parameterized using different tools:
- Discrete approach (fictious load)
- Bezier &
B-Spline curves
- Uniform B-Spline (NURBS)
- Feature-based
solid modeling (in CAD)
In collaboration with DEF, we have decided to parameterize the
shape of the blade using ``Bezier curves''. An illustration of the
parametrization of an airfoil shape using Bezier curves is given
in figures 11.2 and 11.3. The
parametrization of the shape of the blades has been designed by
DEF.
Figure 11.2:
Superposition of thickness normal to camber
to generate an airfoil shape
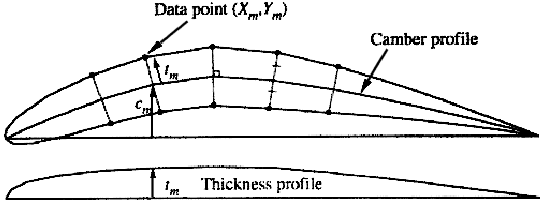 |
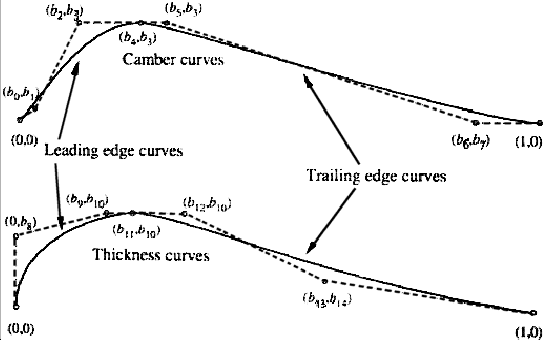
Figure 11.3:
Bezier control variable required to form an
airfoil shape
 |
Some set of shape parameters generates infeasible geometries. The
''feasible space'' of the constrained optimization algorithm is
defined by the set of parameters which generates feasible
geometries. A good parametrization of the shape to optimize should
only involve box or linear constraints. Non-linear constraints
should be avoided.
In the airfoil example, if we want to express that the thickness
of the airfoil must be non-null, we can simply write
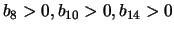 (3 box constraints) (see Figure
11.3 about
(3 box constraints) (see Figure
11.3 about
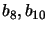 and
and 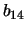 ). Expressing
the same constraint (non-null thickness) in an other, simpler,
parametrization of the airfoil shape (direct description of the
upper and lower part of the airfoil using 2 bezier curves) can
lead to non-linear constraints. The parametrization of the airfoil
proposed here is thus very good and can easily be optimized.
). Expressing
the same constraint (non-null thickness) in an other, simpler,
parametrization of the airfoil shape (direct description of the
upper and lower part of the airfoil using 2 bezier curves) can
lead to non-linear constraints. The parametrization of the airfoil
proposed here is thus very good and can easily be optimized.




Next: Preliminary research
Up: The METHOD project
Previous: The METHOD project
Contents
Frank Vanden Berghen
2004-04-19
