Rosenbrock's optimizer

rosenbrock.cpp

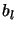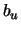This is the core of the Rosenbrock optimizer. The variables $b_l$ and $b_u$ are currently ignored.

#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<memory.h>

char rosenbrock_version[] = "rosenbrock 0.99";

#define MIN(a,b) ((a)<(b)?(a):(b))
#define MAX(a,b) ((a)>(b)?(a):(b))

void rosenbrock(int n, double *x, double *bl, double *bu,
                double bigbnd, int maxiter, double eps, int verbose,
                void obj(int,double *,double *,void *), void *extraparams)
{
    double **xi=(double**)calloc(n,sizeof(double*)),
           *temp1=(double*)calloc(n*n,sizeof(double)),
           **A=(double**)calloc(n,sizeof(double*)),
           *temp2=(double*)calloc(n*n,sizeof(double)),
           *d=(double*)calloc(n,sizeof(double)),
           *lambda=(double*)calloc(n,sizeof(double)),
           *xk=(double*)calloc(n,sizeof(double)),
           *xcurrent=(double*)calloc(n,sizeof(double)),
           *t=(double*)calloc(n,sizeof(double)),
           alpha=2,
           beta=0.5,
           yfirst,yfirstfirst,ybest,ycurrent,mini,div;
    int i,k,j,restart,numfeval=0;

    memset(temp1,0,n*n*sizeof(double));
    for(i=0; i<n; i++)
    {
        temp1[i]=1; xi[i]=temp1; temp1+=n;
                     A[i]=temp2; temp2+=n;
    };
    // memcpy(destination,source,nbre_of_byte)
    memcpy(xk,x,n*sizeof(double));
    for (i=0; i<n; i++) d[i]=.1;
    memset(lambda,0,n*sizeof(double));
    (*obj)(n,x,&yfirstfirst,extraparams); numfeval++;

    do
    {
        ybest=yfirstfirst;
        do
        {
            yfirst=ybest;
            for (i=0; i<n; i++)
            {
                for (j=0; j<n; j++) xcurrent[j]=xk[j]+d[i]*xi[i][j];
                (*obj)(n,xcurrent,&ycurrent,extraparams); numfeval++;
                if (ycurrent<ybest)
                {
                    lambda[i]+=d[i];        // success
                    d[i]*=alpha;
                    ybest=ycurrent;
                    memcpy(xk,xcurrent,n*sizeof(double));
                } else
                {
                    d[i]*=-beta;             // failure
                }
            }
        } while (ybest<yfirst);

        mini=bigbnd;
        for (i=0; i<n; i++) mini=MIN(mini,fabs(d[i]));
        restart=mini>eps;

        if (ybest<yfirstfirst)
        {
            mini=bigbnd;
            for (i=0; i<n; i++) mini=MIN(mini,fabs(xk[i]-x[i]));
            restart=restart||(mini>eps);

            if (restart)
            {
                // nous avons:
                // xk[j]-x[j]=(somme sur i de) lambda[i]*xi[i][j];

                for (i=0; i<n; i++) A[n-1][i]=lambda[n-1]*xi[n-1][i];
                for (k=n-2; k>=0; k--)
                    for (i=0; i<n; i++) A[k][i]=A[k+1][i]+lambda[k]*xi[k][i];

                t[n-1]=lambda[n-1]*lambda[n-1];
                for (i=n-2; i>=0; i--) t[i]=t[i+1]+lambda[i]*lambda[i];
                for (i=n-1; i>0; i--)
                {
                    div=sqrt(t[i-1]*t[i]);
                    if (div!=0)
                        for (j=0; j<n; j++)
                            xi[i][j]=(lambda[i-1]*A[i][j]-xi[i-1][j]*t[i])/div;
                }
                div=sqrt(t[0]);
                for (i=0; i<n; i++) xi[0][i]=A[0][i]/div;

                memcpy(x,xk,n*sizeof(double));
                memset(lambda,0,n*sizeof(double));
                for (i=0; i<n; i++) d[i]=.1;
                yfirstfirst=ybest;
            }
        }
    } while ((restart)&&(numfeval<maxiter));
    // the maximum number of evaluation is approximative
    // because in 1 iteration there is n function evaluations.
    if (verbose)
    {
        printf("ROSENBROCK method for local optimization (minimization)\n"
               "number of evaluation of the objective function= %i\n\n",numfeval);
    }

    free(xi[0]);
    free(A[0]);
    free(d);
    free(lambda);
    free(xk);
    free(xcurrent);
    free(t);
}

rosenbrock.h

#ifndef __INCLUDE__ROSEN_H___ #define __INCLUDE__ROSEN_H___

void rosenbrock(int n, double *x, double *bl, double *bu,
                double bigbnd, int maxiter, double eps, int verbose,
                void obj(int,double *,double *,void *), void *extraparams);

#endif

testR1.cpp

This is an example code where we use the Rosenbrock optimizer to optimize the Rosenbrock banana function.

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <memory.h>
#include "rosenbrock.h"

#define SQR(a) ((a)*(a))

void obj32(int nparam,double *x,double *fj,void *extraparams) {
//   *fj=pow((x[0]-2.0),4.0)+pow((x[0]-2.0*x[1]),2.e0);
    *fj=100*SQR(x[1]-SQR(x[0]))+SQR(1-x[0]);
   return;
}

void message(int n,double *x) {
    double y;
    int i;
    printf("optimum found at:\n");
    for (i=0; i<n; i++)
        printf(" x[%i]=%f\n",i+1,x[i]);
    obj32(n,x,&y,NULL);
    printf("objective function value= %f\n", y);
};

int main() {
    int nparam,maxIter,verbosity;
    double *x,*bl,*bu,bigbnd,eps;

    nparam=2;
    x=(double*)calloc(nparam,sizeof(double));
    bl=(double *)calloc(nparam,sizeof(double));
    bu=(double *)calloc(nparam,sizeof(double));
    bigbnd=1.e10;
    maxIter=5000;
    eps=1.e-5;
    verbosity=1;

    bl[0]=bl[1]=-10;
    bu[0]=bu[1]=10;

    x[0]=5;
    x[1]=5;

    rosenbrock(nparam,x,bl,bu,bigbnd,maxIter,eps,verbosity,obj32,NULL);

    message(nparam,x);

    free(x);
    free(bl);
    free(bu);
    return 0;
}