


Next: Primal-dual interior point
Up: A short review of
Previous: Linear constraints
Contents
Subsections
The material of this section is based on the following reference:
[Fle87].
Consider the following optimization problem:
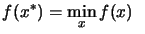 Subject to: Subject to: 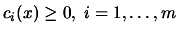 |
(8.5) |
A
penalty function is some combination of 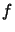 and
and 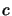 which enables
which enables
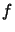 to be minimized whilst controlling constraints violations (or
near constraints violations) by penalizing them. A primitive
penalty function for the inequality constraint problem
8.5 is
to be minimized whilst controlling constraints violations (or
near constraints violations) by penalizing them. A primitive
penalty function for the inequality constraint problem
8.5 is
![$\displaystyle \phi(x, \sigma)= f(x)+\frac{1}{2} \sigma
\sum_{i=1}^{m} [ \min ( c_i(x), 0 )]^2$](img932.png) |
(8.6) |
The penalty parameter
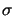 increases from iteration to iteration to ensure that the
final solution is feasible. The penalty function is thus more and
more ill-conditioned (it's more and more difficult to approximate
it with a quadratic polynomial). For these reason, penalty
function methods are slow. Furthermore, they produce infeasible
iterates. Using them for "approach 2" is not possible.
However, for "approach 1" they can be a good alternative,
especially if the constraints are very non-linear.
The material of this section is based on the following references:
[NW99,BV04,CGT00f].
increases from iteration to iteration to ensure that the
final solution is feasible. The penalty function is thus more and
more ill-conditioned (it's more and more difficult to approximate
it with a quadratic polynomial). For these reason, penalty
function methods are slow. Furthermore, they produce infeasible
iterates. Using them for "approach 2" is not possible.
However, for "approach 1" they can be a good alternative,
especially if the constraints are very non-linear.
The material of this section is based on the following references:
[NW99,BV04,CGT00f].
Consider the following optimization problem:
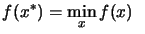 Subject to: Subject to: 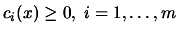 |
(8.7) |
We aggregate the constraints and the objective function in one
function which is:
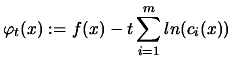 |
(8.8) |
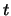 is called the barrier parameter. We will refer to
is called the barrier parameter. We will refer to
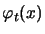 as the barrier function. The degree of
influence of the barrier term "
as the barrier function. The degree of
influence of the barrier term "
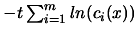 " is
determined by the size of
" is
determined by the size of 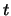 . Under certain conditions
. Under certain conditions 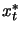 converges to a local solution
converges to a local solution 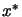 of the original problem when
of the original problem when
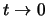 . Consequently, a strategy for solving the
original NLP (Non-Linear Problem) is to solve a sequence of
barrier problems for decreasing barrier parameter
. Consequently, a strategy for solving the
original NLP (Non-Linear Problem) is to solve a sequence of
barrier problems for decreasing barrier parameter 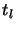 , where
, where 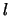 is the counter for the sequence of subproblems. Since the exact
solution
is the counter for the sequence of subproblems. Since the exact
solution
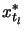 is not of interest for large
is not of interest for large
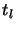 , the corresponding barrier problem is solved only to a
relaxed accuracy
, the corresponding barrier problem is solved only to a
relaxed accuracy
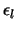 , and the approximate solution is
then used as a starting point for the solution of the next barrier
problem. The radius of convergence of Newton's method applied to
8.8 converges to zero as
, and the approximate solution is
then used as a starting point for the solution of the next barrier
problem. The radius of convergence of Newton's method applied to
8.8 converges to zero as
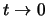 . When
. When
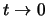 , the barrier function becomes more and more
difficult to approximate with a quadratical function. This lead to
poor convergence speed for the newton's method. The conjugate
gradient (CG) method can still be very effective, especially if
good preconditionners are given. The barrier methods have evolved
into primal-dual interior point which are faster. The relevance of
these methods in the case of the optimization of high computing
load objective functions will thus be discussed at the end of the
section relative to the primal-dual interior point methods.
, the barrier function becomes more and more
difficult to approximate with a quadratical function. This lead to
poor convergence speed for the newton's method. The conjugate
gradient (CG) method can still be very effective, especially if
good preconditionners are given. The barrier methods have evolved
into primal-dual interior point which are faster. The relevance of
these methods in the case of the optimization of high computing
load objective functions will thus be discussed at the end of the
section relative to the primal-dual interior point methods.



Next: Primal-dual interior point
Up: A short review of
Previous: Linear constraints
Contents
Frank Vanden Berghen
2004-04-19
![$\displaystyle \phi(x, \sigma)= f(x)+\frac{1}{2} \sigma
\sum_{i=1}^{m} [ \min ( c_i(x), 0 )]^2$](img932.png)