Rosenbrock Method

The Rosenbrock method

and business-insight
is a 0th order search algorithm (it means it does not require any derivatives of the target function. Only simple evaluations of the objective function are used). Yet, it approximates a gradient search thus combining advantages of 0th order and 1st order strategies. It was published by Rosenbrock(1) in the 70th.

This method is particularly well suited when the objective function does not require a great deal of computing power. In such a case, it's useless to use very complicated optimization algorithms. We will lose our time in the optimization calculations instead of making a little bit more evaluations of the objective function which will lead, at the end, to a shorter
and business-insight
calculation time.

If the objective function takes lots of time to evaluate (more than a few seconds), you should use a more complex algorithm.


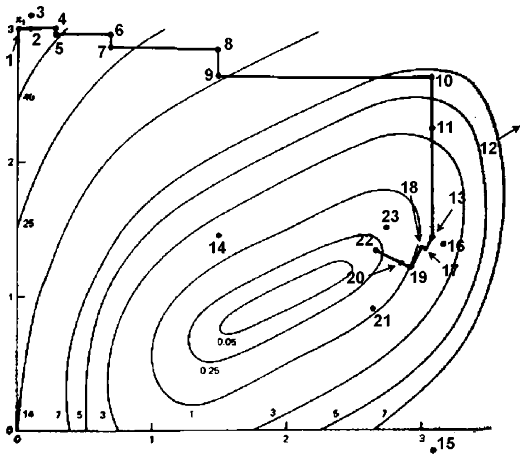
In the first iteration, it is a simple 0th order search in the directions of the base vectors of an n-dimensional coordinate system (in the figure above n=2). In the case of a success, which is an attempt yielding a new minimum value of the target function, the step width is increased, while in the case of a failure it is decreased and the opposite direction will be tried (see points 1 to 16 in the figure above).

and business-insight
Once a success has been found and exploited in each base direction, the coordinate system is rotated in order to make the first base vector point into the direction of the gradient (the points 13,16,&17 are defining the new base in the figure above). Now all step widths are initialized and the process is repeated using the rotated coordinate system (points 16 to 23).

Nelder-Mead Methods (also called non-linear simplex) are very similar to the Rosenbrock Algorithm. However they should be avoided because there is no proof of convergence for these algorithms. In fact, Nelder-Mead Methods can fail to find a local optimum of a very simple optimization problem based on the minimization of a polynomial (4). This is due to degenerescence inside the simplex. Even when no degenerescence occurs, the convergence speed can becomes arbitrarly slow. The Rosenbrock algorithm does not suffer from these problems. The Rosenbrock algorithm has also been proved to always converge (4) (global convergence to a local optima assured). Please, stop using Nelder-Mead Methods! It is slow and do not always converge.

The creation of a new rotated coordinate system is usually done using a Gram-Shmidt orthogonalization procedure. In extreme cases, this algorithm becomes numerically instable. This instabillity can lead to a premature ending of the optimization algorithm. The Gram-Shmidt orthogonalization procedure can also become very time consuming when the dimension n of the search space increases (the complexity of the procedure is n^3). The new orthogonalization procedure of J.R.Palmer (3) solves these issues.

Initializing the step widths to rather big values enables the strategy to leave local optima and to go on with search for more global minima. If you set properly the initial step width, you will find almost always the global optima. If you want to be sure to always find the global optima, you must use a global-search optimization method like, for example: These global-search methods (STEP method, DIRECT method and MCS method) are assuming that the objective function is "fast" to evaluate. If it's not the case, than you should use CONDOR. Inside CONDOR, if you set properly the initial step width (the "rho_start" parameter), you will find almost always the global optima.

It has turned out that the Rosenbrock approach is more stable than many sophisticated algorithms and it requires much less calculations of the target function than higher order strategies (2).

Finally a user who is not an optimization expert has a real chance to understand it and to set and tune its parameters properly.

Bibliography

(1) "An automatic Method for findong the greatest or least Value of a Function", Rosenbrock, H. H., Comp. J., 3, pp 175-184, (1960). The paper is mirrored here.
(2) Schwefel, H.-P., Num. Opt. v. Comp.-modellen m. d. Evol.-strat., Basel, Birkhäuser, 1977.
(3) "An improved procedure for orthogonalising the search vectors in Rosenbrock's and Swann's direct search optimization methods", J.R.Palmer, The Computer Journal, Volume 12, Issue 1, pp. 69-71. The paper is mirrored here.
(4) "Nonlinear Programming: Theory and Algorithms, 2nd Edition", Mokhtar S. Bazaraa, Hanif D. Sherali, C. M. Shetty.
(5) "STEP: The Easiest Way to Optimize a Function", Stephan Langerman, Grégory Seront, Hugues Bersini.
(6) "Direct Optimization Algortihm", Daniel E. Finkel. A local copy of a paper describing the method is here.
(7) "Gloabl optimization by multilvel Coordinate Search", Waltraud Huyer, Arnold Neumaier. A local copy of a paper describing the method is here.

Links & Download

The original paper by Rosenbrock is available online here. It is mirrored here

and business-insight
.
The paper describing the improvement of JR.Palmer is available here. The paper is mirrored here.
Some "bonus" material: a discussion about convergence speed of the algorithm.

The code of my implementation of the Rosenbrock algorithm is available here. The code of the optimizer is standard C and doesn't use any special libraries. It can be compiled under windows or unix without any problem. The code has been highly optimized to be as fast as possible (with extend use of memcpy function, special fast matrix manipulation and so on...). The improvement of J.R. Palmer is used. This improvement allows still faster speed (the complexity of the orthogonalization procedure of J.R.Palmer is only n^2). The whole algorithm is only 107 lines long (with correct indentations). It's written in pure structural programmation (there is no goto instruction). It is thus very easy to understand/customize. A small example of use (testR1.cpp) is available. In this example, the standard Rosenbrock banana function is minimized.