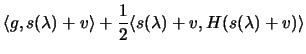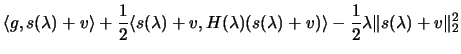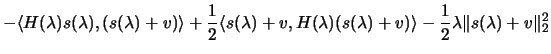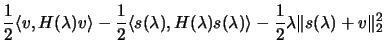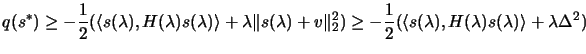Next: An estimation of the
Up: The Trust-Region subproblem
Previous: The Rayleigh quotient trick
Contents
Subsections
In other words, if 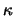 is small, then the reduction in
is small, then the reduction in 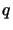 that occurs at the point
that occurs at the point 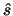 is close to the greatest
reduction that is allowed by the trust region
constraint.
is close to the greatest
reduction that is allowed by the trust region
constraint.
Proof
for any 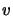 , we have the identity:
, we have the identity:
If we choose 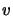 such that
such that
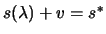 , we have:
, we have:
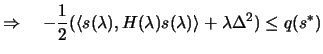 |
(4.24) |
From 4.27, using the 2 hypothesis:
Combining 4.28 and 4.29, we obtain finally
4.26.
Lemma
From the hypothesis:
Combining 4.31 and 4.27 when 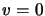 reveals that:
reveals that:
The required inequality 4.30 is immediate from
4.28 and 4.32.
We will use this lemma with
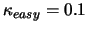 .
We will choose
.
We will choose 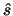 as (see paragraph containing Equation
4.15 for the meaning of
as (see paragraph containing Equation
4.15 for the meaning of 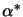 and
and 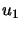 ):
):
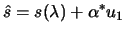 |
(4.28) |
Thus, the condition for
ending the trust region calculation simplifies to the inequality:
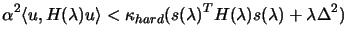 |
(4.29) |
We will choose
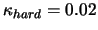 .
.




Next: An estimation of the
Up: The Trust-Region subproblem
Previous: The Rayleigh quotient trick
Contents
Frank Vanden Berghen
2004-04-19