next up previous contents
Next: Preliminary research Up: The METHOD project Previous: The METHOD project   Contents

Parametrization of the shape of the blades

A shape can be parameterized using different tools: In collaboration with DEF, we have decided to parameterize the shape of the blade using ``Bezier curves''. An illustration of the parametrization of an airfoil shape using Bezier curves is given in figures 11.2 and 11.3. The parametrization of the shape of the blades has been designed by DEF.

Figure 11.2: Superposition of thickness normal to camber to generate an airfoil shape
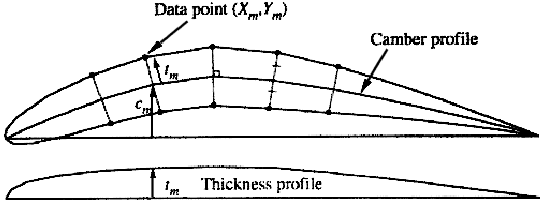\begin{figure} \centering\epsfig{figure=figures/bezier.eps, width=12cm, height=4.5cm} \end{figure}

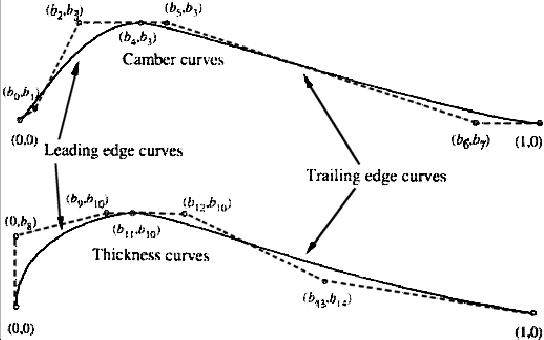
Figure 11.3: Bezier control variable required to form an airfoil shape
\begin{figure} \centering\epsfig{figure=figures/bezier2.eps, width=12cm, height=7.5cm} \end{figure}

Some set of shape parameters generates infeasible geometries. The ''feasible space'' of the constrained optimization algorithm is defined by the set of parameters which generates feasible geometries. A good parametrization of the shape to optimize should only involve box or linear constraints. Non-linear constraints should be avoided.
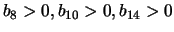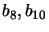In the airfoil example, if we want to express that the thickness of the airfoil must be non-null, we can simply write $ b_8>0, b_{10}>0, b_{14}>0$ (3 box constraints) (see Figure 11.3 about $ b_8, b_{10}$ and $ b_{14}$). Expressing the same constraint (non-null thickness) in an other, simpler, parametrization of the airfoil shape (direct description of the upper and lower part of the airfoil using 2 bezier curves) can lead to non-linear constraints. The parametrization of the airfoil proposed here is thus very good and can easily be optimized.
next up previous contents
Next: Preliminary research Up: The METHOD project Previous: The METHOD project   Contents
Frank Vanden Berghen 2004-04-19