FUZZY CONTROL
In the year 2000, I worked with 2 colleagues (Antoine
Duchâteau and Edy
Bertolissi) on the European LTR projet FAMIMO
(FAMIMO stands for "Fuzzy Algorithms for the Control of Multi-Input, Multi-Output
Processes"). The main goal of this project was to see if the fuzzy control
is a viable alternative to the classical PID control. Apparently the answer
is no. During the project, we develloped the NLMIMO
toolbox. The NLMIMO toolbox is composed of two main modules:
- an identification module using (fuzzy/ lazy learning/ classical linear)
techniques.
- a multiple input, multiple ouput, multiple step ahead, direct self-adaptive
fuzzy controller.
The first module has been implemented by Antoine
Duchâteau. The second module has been mainly programmed by myself. The
controller is from a GPC type (global predictive control). GPC controllers
simulate the process to control in the future using prediction/identification
techniques. Based on this simulation, we can calculate the error E
between the setpoints and the real ouput of the process. This error E
is a function depending on the control signals u
generated by the controller. These signals u
themselves depend on the parameter w
of the fuzzy rules inside the controller. Thus, we will try to find the value
of w which minimize the error
E(u(w)). The
minimization algorithm (the optimization
algorithm) is a simple "steppest descent step" (see my thesis
about optimization). This learining algorithm is used on-line. The controller
is thus adaptative. Due to this property the controller could be able to rapidly
absorb unexpected perturbations.
GPC controllers have often some difficulties with minimum phase systems. In
these kind of systems, we must first increase the error E,
in order to reach the setpoint. One example of such system is the well known
inverted pendulum system.
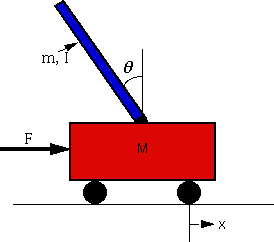
The inverted Pendulum System
The red box underneath is a roller cart controlled by a motor that pulls
it to the left or right according to the controller's command. A blue pendulum
is attached on top of the roller cart. The goal of the controller is to use
the motor to keep the pendulum in balance (vertical) and the roller cart at
a precise x* position. If
the current position is x,
than the current regulation error is E=abs(x-x*).
In order to reach a new x position,
we must first balance the pendulum a little in the opposite direction of the
new position (see the applet below). This will temporarly increase the error
E. A simple GPC wich is only
able to look 1 step in the future will be unable to control the system. A
multiple-step-ahead GPC controller will (at the condition that the prediction
horizon is not too short) have no problem.
You can see an example of control of an inverted pendulum in the java applet
above. The blue line is the current x
position of the cart. The green line is the control signal u
(that is: the torque applied on the wheels). It is interesting to notice the
typical pattern present in the non minimum phase systems: At each set point
change, the system starts in the opposite direction with respect to the current
value of the reference signal.
The multiple-step-ahead direct adaptative
fuzzy controller
The regulator develloped in IRIDIA is able to simulate the behavior of the
process to control using (fuzzy/ lazy learning/ classical linear) predictors
(or a mix of them, one different predictor for each output of the system to
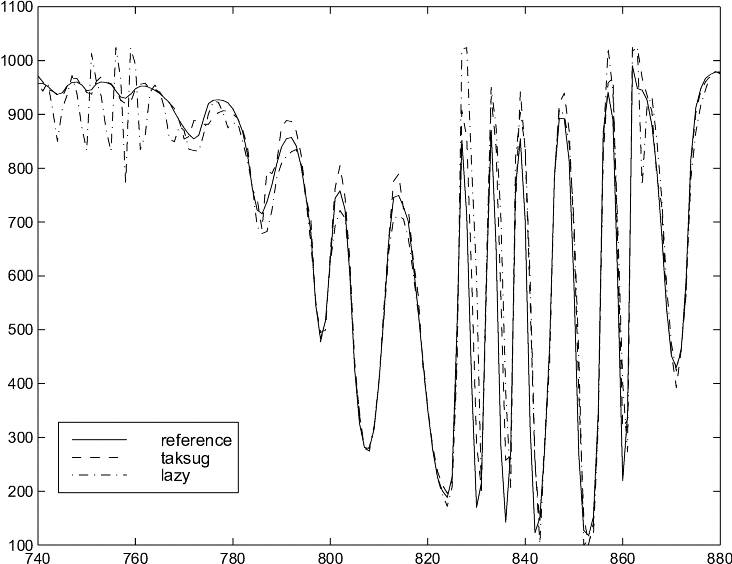
control). The lazy learning predictor can be trained on-line as illustrated
in the figure below (manifold pressure control in a Gasoline
Direct Injection engine(GDI)). The TAKSUG line stands for Takagi Sugeno
fuzzy sets predictor. The LAZY line stands for the lazy learning
predictor.
Another example is the control of this simple toy problem: 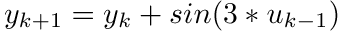 .
.
The result is the following:
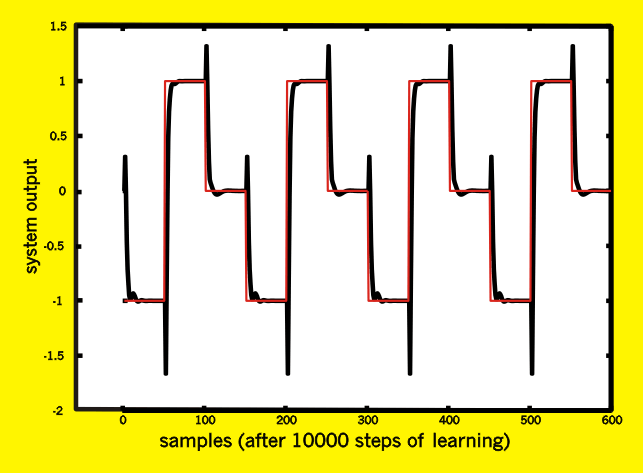
Once again, note the typical pattern present in the non minimum phase systems
Bibliography
"Edy Bertolissi, Antoine Duchâteau, Hugues Bersini, Frank Vanden Berghen.
Direct Adaptive Fuzzy Control for MIMO Processes, Accepted to the FUZZ-IEEE
2000 conference, San Antonio, Texas, 7-10 May, 2000" is downloadable
here.
Download
"Edy Bertolissi, Antoine Duchâteau, Hugues Bersini, Frank Vanden Berghen.
Direct Adaptive Fuzzy Control for MIMO Processes, Accepted to the FUZZ-IEEE
2000 conference, San Antonio, Texas, 7-10 May, 2000" is downloadable
here.
A chapter of a book
in french on fuzzy control is downloadable here.
An internal IRIDIA report describing in more depth the algorithm is available
here
(only in French).
A paper describing the identification modules of the NLMIMO toolbox is here.
The latest version of the NLMIMO toolbox (july 2000) is here.
You must have matlab 5.0, 5.1 or 5.2 to have all functionalities. In matlab
5.3, the control modules are not functioning. In matlab 6.0, nothing works
(there is a conflict between the name of the new function called 'system'
in matlab and the name of the 'system' class).
Links
An on-line
book on control theory with many examples in java applets.
A revolutionary methodology for optimal control : the Q-learning.
R. Babuska. Fuzzy
Modeling for Control. Kluwer Academic Publishers, Boston, 1998.
HANUS, Raymond ; BOGAERTS, Philippe, Introduction à l'automatique.
1, systèmes continus
Bruxelles : De Boeck Université 1996, 312 p.ISBN: 2-8041-2108-9 is
an excellent french book. You can order it here.
HANUS, Raymond ; BOGAERTS, Philippe , Introduction à l'automatique.
2, systèmes discrets et échantillonnés
Bruxelles : De Boeck Université 2000, 296 p. ISBN: 2-8041-2368-5 is
an excellent french book. You can order it here.


![]() .
.